
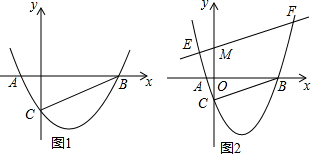
分析 (1)先求出B、C两点坐标,利用待定系数法即可解决问题.
(2)如图1中,设P(m,am2-2am-3a).构建二次函数,利用二次函数的性质,列出方程即可解决问题.
(3)如图2中,作EH⊥y轴于H,FG⊥EH交EH的延长线于G.不妨设直线EF的解析式为y=ax+b,E(x1,y1),F(x2,y2),由$\left\{\begin{array}{l}{y=ax+b}\\{y=a{x}^{2}-2ax-3a}\end{array}\right.$消去y得到ax2-3ax-3a-b=0,推出x1+x2=-$\frac{-3a}{a}$=3,推出HG-EH=3,由HM∥GF,推出$\frac{MF}{ME}$=$\frac{HG}{HE}$,推出$\frac{MF+ME}{MF-ME}$=$\frac{HG+EG}{HG-HE}$,推出$\frac{EF}{EG}$=$\frac{MF-ME}{HG-EH}$,由△OBC∽△GEF,推出$\frac{OB}{EG}$=$\frac{BC}{EF}$,推出$\frac{EF}{EG}$=$\frac{BC}{OB}$,推出$\frac{BC}{OB}$=$\frac{MF-ME}{HG-EH}$,推出$\frac{BC}{MF-ME}$=$\frac{OB}{HG-EH}$=$\frac{3}{3}$=1.
解答 解:(1)对于抛物线y=ax2-2ax-3a,令y=0,则有ax2-2ax-3a=0,解得x=-1或3,
∴A(-1,0),B(3,0),
令x=0,得到y=-3a,
∴C(0,-3a),
设直线BC的解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=-3a}\\{3k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=a}\\{b=-3a}\end{array}\right.$,
∴直线BC的解析式为y=ax-3a.
(2)如图1中,设P(m,am2-2am-3a).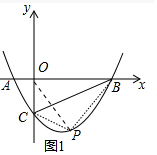
∵S△PBC=S△POC+S△POB-S△BCO=$\frac{1}{2}$×3×(-am2+2am+3a)+$\frac{1}{2}$×3a×m-$\frac{1}{2}$×3×3a
=-$\frac{3}{2}$am2+$\frac{3}{2}$am,
由题意,$\frac{-(\frac{3}{2}\\;a)^{2}}{4(-\frac{3}{2}a)}$=$\frac{27}{16}$,
解得a=$\frac{9}{2}$.
(3)如图2中,作EH⊥y轴于H,FG⊥EH交EH的延长线于G.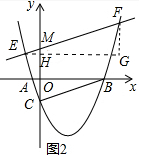
∵直线BC的解析式为y=ax-3a,EF∥BC,
不妨设直线EF的解析式为y=ax+b,E(x1,y1),F(x2,y2),
由$\left\{\begin{array}{l}{y=ax+b}\\{y=a{x}^{2}-2ax-3a}\end{array}\right.$消去y得到ax2-3ax-3a-b=0,
∴x1+x2=-$\frac{-3a}{a}$=3,
∴HG-EH=3,
∵HM∥GF,
∴$\frac{MF}{ME}$=$\frac{HG}{HE}$,
∴$\frac{MF+ME}{MF-ME}$=$\frac{HG+EG}{HG-HE}$,
∴$\frac{EF}{EG}$=$\frac{MF-ME}{HG-EH}$,
易证△OBC∽△GEF,
∴$\frac{OB}{EG}$=$\frac{BC}{EF}$,
∴$\frac{EF}{EG}$=$\frac{BC}{OB}$,
∴$\frac{BC}{OB}$=$\frac{MF-ME}{HG-EH}$,
∴$\frac{BC}{MF-ME}$=$\frac{OB}{HG-EH}$=$\frac{3}{3}$=1.
点评 本题考查二次函数综合题、一次函数的应用、最值问题、相似三角形的判定和性质、一元二次方程的根与系数的关系,比例的性质等知识,解题的关键是学会构建二次函数,利用二次函数的性质解决最值问题,学会添加常用辅助线,构造相似三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | m2-(2m-n-p)=m2-2m+n+p | B. | m-n+p-q=m-(n+q-p) | ||
| C. | 3m-5n-1+2p=-(-3m)-[5n-(2p-1)] | D. | m+1-(-n+p)=-(-1+n-m+p) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | -8 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
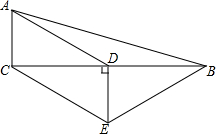 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 变大 | B. | 变小 | C. | 不变 | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了审核书稿中的错别字,选择抽样调查 | |
| B. | 为了了解春节联欢晚会的收视率,选择普查 | |
| C. | “经过由交通信号灯的路口,遇到红灯”是必然事件 | |
| D. | “射击运动员射击一次,命中靶心”是随机事件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com