
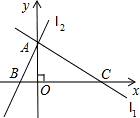
 如图,直线L1交直线L2于y轴上一点A(0,6),交x轴上另一点C.l2交x轴于另一点B,二次函数y=ax2-6ax-16a (a>0)的图象过B、C两点,点P是线段OC上由O向C移动的动点,线段OP=t(1<t<8)
如图,直线L1交直线L2于y轴上一点A(0,6),交x轴上另一点C.l2交x轴于另一点B,二次函数y=ax2-6ax-16a (a>0)的图象过B、C两点,点P是线段OC上由O向C移动的动点,线段OP=t(1<t<8)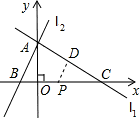 解:(1)抛物线的解析式中,当y=0时,0=a(x2-6x-16),解得:x1=-2,x2=8;
解:(1)抛物线的解析式中,当y=0时,0=a(x2-6x-16),解得:x1=-2,x2=8;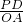 =
= ,即
,即 =
=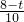
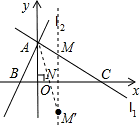 (2)由(1)知:抛物线的对称轴 x=3;
(2)由(1)知:抛物线的对称轴 x=3; x+6,则 M(3,
x+6,则 M(3, ).
). );
); ,k=-
,k=-
 x+6
x+6 ;即 N(
;即 N( ,0).
,0).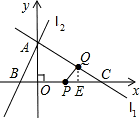 (3)过Q作QE⊥x轴于点E,则 QE=
(3)过Q作QE⊥x轴于点E,则 QE= QE=
QE= t,CE=
t,CE= QC=
QC= t,OE=OC-CE=8-
t,OE=OC-CE=8- t;
t; t,
t, t).
t). PC•QE=
PC•QE= ×(8-t)×
×(8-t)× t=-
t=- t2+
t2+ t(1<t<8).
t(1<t<8). t-t)2+(
t-t)2+( t)2=
t)2= t2-
t2-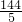 t+64,PC2=(8-t)2=t2-16t+64,CQ2=t2;
t+64,PC2=(8-t)2=t2-16t+64,CQ2=t2; t2-
t2-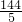 t+64=t2-16t+64,解得:t1=0(舍去),t2=
t+64=t2-16t+64,解得:t1=0(舍去),t2=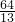 ;
; t2-
t2-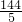 t+64=t2,解得:t1=8(舍去),t2=
t+64=t2,解得:t1=8(舍去),t2=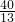 ;
;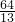 、t2=
、t2=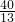 、t3=4.
、t3=4.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
 (2012•荆州模拟)如图,直线L1交直线L2于y轴上一点A(0,6),交x轴上另一点C.l2交x轴于另一点B,二次函数y=ax2-6ax-16a (a>0)的图象过B、C两点,点P是线段OC上由O向C移动的动点,线段OP=t(1<t<8)
(2012•荆州模拟)如图,直线L1交直线L2于y轴上一点A(0,6),交x轴上另一点C.l2交x轴于另一点B,二次函数y=ax2-6ax-16a (a>0)的图象过B、C两点,点P是线段OC上由O向C移动的动点,线段OP=t(1<t<8)查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
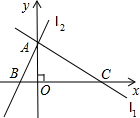
 ,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
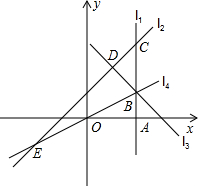 如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2,垂足为D,过点O,B的直线l4交l2于点E,当直线l1,l2,l3能围成三角形时,设该三角形面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形面积为S2.
如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2,垂足为D,过点O,B的直线l4交l2于点E,当直线l1,l2,l3能围成三角形时,设该三角形面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形面积为S2. S1,则∠BOA的度数为______.
S1,则∠BOA的度数为______.查看答案和解析>>
科目:初中数学 来源:2012年湖北省荆州市中考数学调研试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com