
分析 根据铺设客厅每平米的费用=铺设每平米的瓷砖的工钱+每平米瓷砖的价钱,铺设居室每平米的费用=铺设每平米的木质地板的工钱+每平米木质地板的价钱,来列方程组求解.
解答 解:设铺木质地板的工钱为a元/平方米,那么铺瓷砖的工钱为(a+10)元/平方米,
设购买1m2木质地板费用是b元,那么购买1m2的瓷砖的费用是$\frac{3}{4}$b元.根据题意有:
$\left\{\begin{array}{l}{50a+b=10500}\\{30(a+10)+\frac{3}{4}b=5100}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=206}\\{b=200}\end{array}\right.$,
答:购买每平方米木质地板的费用为200元,购买每平方米瓷砖的费用为150元.
点评 本题主要考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程组,再求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
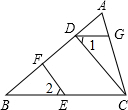 如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.
如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
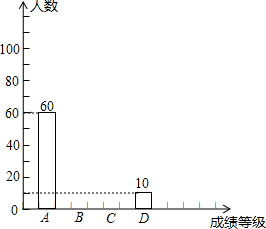 为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:
为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:| 成绩等级 | A | B | C | D |
| 人数 | 60 | x | y | 10 |
| 占抽查学生总数的百分比 | 30% | 50% | 15% | m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
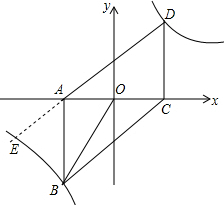 如图,在平面直角坐标系中,点 A、C关于原点O对称,分别过点A、C作x轴的垂线,它们与反比例函数y=$\frac{k}{x}$的图象交于点B、D,连结AD、BC,若C点的坐标为(m,0)
如图,在平面直角坐标系中,点 A、C关于原点O对称,分别过点A、C作x轴的垂线,它们与反比例函数y=$\frac{k}{x}$的图象交于点B、D,连结AD、BC,若C点的坐标为(m,0)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com