
 ,
, ) 是否是线段AB的“邻近点”,并说明理由;
) 是否是线段AB的“邻近点”,并说明理由;
 ,
, ) 是线段AB的“邻近点”。理由如下:
) 是线段AB的“邻近点”。理由如下: -1=
-1= ,∴点C(
,∴点C( ,
, )在直线y=x-1上.。
)在直线y=x-1上.。 ,
, ) 到线段AB的距离是3-
) 到线段AB的距离是3- =
= 。
。 <1,∴C(
<1,∴C( ,
, )是线段AB的“邻近点”。
)是线段AB的“邻近点”。 ,
, )满足“邻近点”的条件即可。
)满足“邻近点”的条件即可。

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源:不详 题型:解答题
| 月份 | 用水量(吨) | 水费(元) |
| 4 | 22 | 51 |
| 5 | 20 | 45 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.-4<b<8 | B.-4<b<0 | C.b<-4或b>8 | D.-4≤6≤8 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
. 为何值时,一次函数的值大于反比例函数的值?
为何值时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| | 甲 | 乙 |
| 维生素A(单位/千克) | 300 | 500 |
| 维生素B(单位/千克) | 700 | 100 |
| 成本(元/千克) | 5 | 4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 轴上,顶点B的坐标为(4,6).若直线
轴上,顶点B的坐标为(4,6).若直线 将□ABCO分割成面积相等的两部分,则k的值是( )
将□ABCO分割成面积相等的两部分,则k的值是( )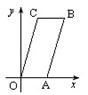
A. | B. | C.- | D.- |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的图象如右图所示,则结论:
的图象如右图所示,则结论: 的坐标为
的坐标为 ; ②当
; ②当 时,
时, ;
;  时,
时, ; ④当
; ④当 逐渐增大时,
逐渐增大时, 随着
随着 的增大而增大,
的增大而增大, 随着
随着 的增大而减小.
的增大而减小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com