
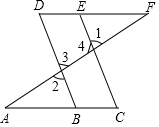
 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.分析 根据已知条件∠1=∠2及对顶角相等求得同位角∠2=∠3,从而推知两直线DB∥EC,所以同位角∠C=∠ABD;然后由已知条件∠C=∠D推知内错角∠D=∠ABD,所以两直线AC∥DF.
解答 证明:∵∠1=∠2,(已知)
∠2=∠3,(对顶角相等)
∠1+∠4=180°(邻补角定义)
∴∠3+∠4=180° (等量代换)
∴DB∥CE(同旁内角互补,两直线平行)
∴∠C=∠ABD (两直线平行,同位角相等)
∵∠C=∠D(已知)
∴∠D=∠ABD (等量代换)
∴DF∥A C (内错角相等,两直线平行)
故答案为:对顶角相等;邻补角定义;DB;CE;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.
点评 本题考查了平行线的性质和判定的应用,能正确运用性质进行推理和计算是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 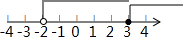 | B. | 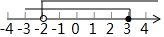 | ||
| C. | 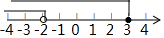 | D. | 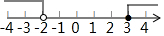 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
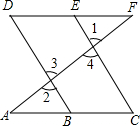 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com