
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
将一块长18米,宽15米的矩形荒地修建成一个花园(阴影部分)所占的面积为原来荒地面积的三分之二.(精确到0.1m)
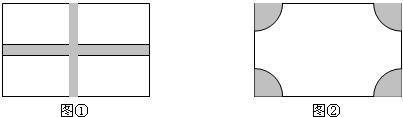
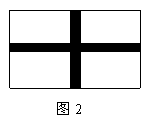
(1)设计方案1(如图2)花园中修两条互相垂直且宽度相等的小路.
(2)设计方案2(如图3)花园中每个角的扇形都相同.
以上两种方案是否都能符合条件?若能,请计算出图2中的小路的宽和图3中扇形的半径;若不能符合条件,请说明理由.
 |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com