
在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A、B的横坐标分别为a+2与2a﹣5,且关于y轴对称,BC的长为3,且点C在第三象限.
(1)求顶点A、C的坐标;
(2)若y=kx+b是经过点B,且与AC平行的一条直线,试确定它的解析式.
(1)A(3,0),C(﹣3,﹣3);(2)
解析试题分析:(1)根据关于y轴对称的点的坐标特征得到a+2+2a﹣5=0,解得a=1,则得到A点坐标为(3,0),B定坐标为(﹣3,0),然后利用矩形的性质和BC=3可得到C点坐标;(2)先利用待定系数法确定直线AC的解析式,然后利用一次函数图象与几何变换求解.
试题解析:(1)∵点A与点B关于y轴对称,
∴a+2+2a﹣5=0,解得a=1,
∴A点坐标为(3,0),B定坐标为(﹣3,0),
∵矩形ABCD的边BC=3,
∴C点坐标为(﹣3,﹣3);
(2)设直线AC的解析式为y=mx+n,
把A(3,0)、(﹣3,﹣3)代入得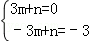 ,
,
解得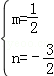 ,
,
∴直线AC的解析式为 ,
,
∵把直线AC向上平移3个单位得到过B点的直线,
∴经过点B,且与AC平行的直线解析式为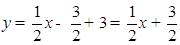 .
.
考点:1.待定系数法求一次函数解析式;2.一次函数图象与几何变换


科目:初中数学 来源: 题型:解答题
如图,直线y=﹣x+5分别与x轴、y轴交于A、B两点.
(1)求A、B两点的坐标;
(2)已知点C坐标为(4,0),设点C关于直线AB的对称点为D,请直接写出点D的坐标;
(3)请在直线AB和y轴上分别找一点M、N使△CMN的周长最短,在平面直角坐标系中作出图形,并求出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,樱桃价格z(单位:元/千克)与上市时间x(单位:天)的函数关系如图2所示。
(1)观察图象,直接写出日销售量的最大值;
(2)求李明家樱桃的日销售量y与上市时间x的函数解析式;
(3)试比较第10天与第12天的销售金额哪天多?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如表,给出A、B两种上网宽带的收费方式:
| 收费方式 | 月使用费/元 | 包月上网时间/小时 | 超时费/(元/分) |
| A | 30 | 20 | 0.05 |
| B | 60 | 不限时 | |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某校校长暑假带领该市市级“三好学生”去北京旅游.甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说:“包括校长在内的全部按全票价的6折优惠”(即按全票的60%收费).若全票价为240元/人,
(1)设学生人数为x,甲旅行社收费为y甲,乙旅行社收费为y乙,分别计算两家旅行社的收费(建立表达式).
(2)当学生人数为多少时,两家旅行社的收费一样?
(3)就学生人数讨论哪家旅行社更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:甲、乙两车分别从相距300千米的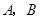 两地同时出发相向而行,其中甲到
两地同时出发相向而行,其中甲到 地后立即返回,下图是它们离各自出发地的距离
地后立即返回,下图是它们离各自出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象.
(1)求甲车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,并写出自变量的取值范围;
(小时)之间的函数关系式,并写出自变量的取值范围;
(2)当它们行驶到与各自出发地的距离相等时,用了 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式;
(小时)之间的函数关系式;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.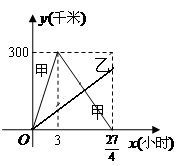
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com