练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    阅读下面的问题：

    (1)一位居民打电话给供电部门反映“前进路第8个电杆的路灯坏了”，维修人员很快修好了路灯．

    (2)某人买了一张5排9号的电影票，很快找到了自己的座位．

    (3)地质部门在某地埋下一个标志牌，上面写着“北纬44.2°，东经125.7°”．

    请分析上面几个问题有什么共同的特点？

    答案：
    解析：

    上面这几个问题中都是用两个量来确定平面上一个点的位置．如(1)中“××路×个电线杆”，(2)中“×排×号”，(3)中“北纬×度，东经×度”，都是用两个量确定一个点的位置．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    27、先阅读下面的问题：
    在实际生活中常见到求平均数的问题．例如：
    问题某校初一级篮球队12名同学的身高（厘米）分别如下：171，168，170，173，165，178，166，161，176，172，176，176．
    求全队同学的平均身高．
    解：分别将各数减去170，得1，-2，0，3，-5，8，-4，-9，6，2，6，6
    这组数的平均数为：（1-2+0+3-5+8-4-9+6+2+6+6）÷12=12÷12=1
    则已知数据的平均数为：170+1=171
    答：全队同学的平均身高为171厘米．
    通过阅读上面解决问题的方法，请利用它解决下面的问题：
    （1）10筐苹果称重（千克）如下：32，26，32.5，33，29.5，31.5，33，29，30，27.5问这10筐苹果的平均重量是多少
    （2）若有一组数为：a-1，a+5，a-1，a-2，a-4，a+1，a+2，这组数的平均数为
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    请仔细阅读下面的问题：
    		3
    		3
    -
    		2
    =
    		3
    (
    		3
    +
    		2
    )
    (
    		3
    -
    		2
    )(
    		3
    +
    		2
    )
    =
    3+
    		6
    (
    		3
    )    2    -(
    		2
    )    2
    =3+
    		6

    像上面解题中，
    		3
    -
    		2
    与
    		3
    +
    		2
    相乘，积不含二次根式，称
    		3
    -
    		2
    与
    		3
    +
    		2
    为互为有理化因式，化去分母中的根式而使原式的大小不变称为分母有理化．
    根据上面的数学思想方法，完成下面各题：
    （1）写出
    		7
    -
    		5
    的一个有理化因式：
     
    ．
    （2）将
    2
    		3
    -
    		5
    分母有理化得：
     
    ．
    （3）计算：
    1
    		n+1
    +
    		n
    +
    		n
    （n为非负整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读下面的问题及解答．
    已知：如图①，在△ABC中，∠ABC、∠ACB的角平分线交于O点，则∠BOC=90°+
    1
    2
    ∠A=
    1
    2
    ×180°+
    1
    2
    ∠A；
    如图②，在△ABC中，∠ABC、∠ACB的三等分线交于O1、O2，则∠BO1C=
    2
    3
    ×180°+
    1
    3
    ∠A，∠BO2C=
    1
    3
    ×180°+
    2
    3
    ∠A，
    根据以上信息，回答下列问题：
    精英家教网
    （1）你能猜想出它的规律吗？（n等分时，内部有n-1个点）．∠BO1C=
     
    （用n的代数式表示），
    ∠BOn-1C=
     
    （图③）．
    （2）根据你的猜想，取n=4时，证明∠BO3C的度数成立．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    加试题（本小题满分20分，其中（1）、（2）、（3）题各3分，（4）题11分）
    （1）一个正数的平方根为3-a和2a+3，则这个正数是
    81
    81

    （2）若x2+2x+y2-6y+10=0，则xy=
    -1
    -1

    （3）已知a，b分别是6-
    		13
    的整数部分和小数部分，则2a-b=
    		13
    		13

    （4）阅读下面的问题，并解答问题：
    1）如图1，等边△ABC内有一点P，若点P到顶点A，B，C的距离分别为3，4，5，求∠APB的度数是多少？（请在下列横线上填上合适的答案）
    分析：由于PA，PB，PC不在同一个三角形中，为了解决本题我们可以将△ABP绕顶点A逆时针旋转到△ACP′处，此时可以利用旋转的特征等知识得到：
      ①∠APB=∠AP′C=∠AP′P+∠PP′C；
      ②AP=AP′，且∠PAP′=
    60
    60
    度，所以△APP′为
    等边
    等边
    三角形，则∠AP′P=
    60
    60
    度；
      ③P′C=BP=4，P′P=AP=3，PC=5，所以△PP′C为
    直角
    直角
    三角形，则∠PP′C=
    90
    90
    度，从而得到∠APB=
    150
    150
    度．
     2）请你利用第1）题的解答方法，完成下面问题：
    如图2，在△ABC中，∠CAB=90°，AB=AC，E、F为边BC上的点，且∠EAF=45°，试说明：EF2=BE2+FC2．

    查看答案和解析>>

    科目：初中数学 来源：2008-2009学年山东省菏泽市郓城县九年级（上）期末数学试卷（解析版） 题型：解答题

    请仔细阅读下面的问题：
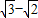    像上面解题中，与相乘，积不含二次根式，称与为互为有理化因式，化去分母中的根式而使原式的大小不变称为分母有理化．
    根据上面的数学思想方法，完成下面各题：
    （1）写出的一个有理化因式：______

    查看答案和解析>>

    同步练习册答案