解:(1)猜想:若方程x
2+px+q=0(p、q是常数,x是未知数)有两个根x
1、x
2,则x
1+x
2=-p,x
1•x
2=q.理由如下:
∵方程x
2+px+q=0的两实根是x
1=

,x
2=

,
∴x
1+x
2=

+

=

=-p,
x
1•x
2=

•

=
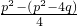
=q;
(2)∵α、β是方程x
2+(m-2)x+502=0的两根,
∴α
2+(m-2)α+502=0,β
2+(m-2)β+502=0,
∴α
2+mα=2α-502,β
2+mβ=2β-502,
又由(1)知,α+β=2-m,αβ=502,
∴(502+mα+α
2)(502+mβ+β
2)=(502+2α-502)(502+2β-502)=4αβ=2008.
分析:(1)观察方程的两根的和与积与方程的系数之间的关系,利用系数表示出两个根的和与积得到结论,然后利用求根公式进行证明;
(2)先根据方程根的定义得出α
2+(m-2)α+502=0,β
2+(m-2)β+502=0,变形之后,再利用(1)的结论求出即可.
点评:本题考查了学生的阅读理解能力及知识的迁移能力,实际上考查了根与系数的关系,求根公式及方程的解的定义,难度中等.

 ,x2=
,x2= ,则x1+x2=1,x1•x2=-1
,则x1+x2=1,x1•x2=-1 ,x2=
,x2= ,
, +
+ =
= =-p,
=-p, •
• =
=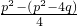 =q;
=q;

 一本好题口算题卡系列答案
一本好题口算题卡系列答案