
 ABCD是正方形,∠MAN=45°,NG∥AD,求证:MN=$\sqrt{2}$PQ;CM=$\sqrt{2}$DQ;CN=$\sqrt{2}$BP;△AQM,△APN为等腰直角三角形.
ABCD是正方形,∠MAN=45°,NG∥AD,求证:MN=$\sqrt{2}$PQ;CM=$\sqrt{2}$DQ;CN=$\sqrt{2}$BP;△AQM,△APN为等腰直角三角形. 分析 先有∠MAN=45°得出∠MAC=∠DAN,结合∠ACM=∠ADQ,得出△AMC∽△AQD,得到比例式判断出CM=$\sqrt{2}$DQ,同理:得出CN=$\sqrt{2}$BP,由$\frac{AQ}{AM}=\frac{AD}{AC}$=$\frac{DQ}{CM}$=$\frac{\sqrt{2}}{2}$①
和$\frac{AP}{AN}=\frac{AB}{AC}$=$\frac{BP}{CN}$=$\frac{\sqrt{2}}{2}$②,得出$\frac{AQ}{AM}=\frac{AP}{AN}$,从而判断出△APQ∽△ANM即可得出MN=$\sqrt{2}$PQ,再由∠MAQ=∠MBQ=45°,得到点A,B,M,Q四点共圆,即可判断出∠AQM=90°,即得到△AQM为等腰直角三角形.同理得出△APN为等腰直角三角形.
解答 解: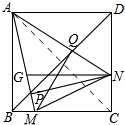
连接AC,
∵AC,BD是正方形ABCD的对角线,
∴∠CBD=∠BDC=∠ACB=45°,∠ABC=∠ADC=90°,AC=$\sqrt{2}$AD=$\sqrt{2}$AB,
∵∠MAN=45°,
∴∠MAC+∠CAN=∠DAN+∠CAN,
∴∠MAC=∠DAN,
∵∠ACM=∠ADQ=45°,
∴△AMC∽△AQD,
∴$\frac{AQ}{AM}=\frac{AD}{AC}$=$\frac{DQ}{CM}$=$\frac{\sqrt{2}}{2}$①,
∴CM=$\sqrt{2}$DQ,
同理:△APB∽△ANC,
∴$\frac{AP}{AN}=\frac{AB}{AC}$=$\frac{BP}{CN}$=$\frac{\sqrt{2}}{2}$②,
∴CN=$\sqrt{2}$BP,
由①②得,$\frac{AQ}{AM}=\frac{AP}{AN}$,
∵∠PAQ=∠NAM,
∴△APQ∽△ANM,
∴$\frac{PQ}{MN}=\frac{AQ}{AM}$=$\frac{\sqrt{2}}{2}$,
∴MN=$\sqrt{2}$PQ,
∵∠MAQ=∠MBQ=45°,
∴点A,B,M,Q四点共圆,
∴∠ABM+∠AQM=180°,
∵∠ABM=90°,
∴∠AQM=90°,
∵∠MAQ=45°,
∴△AQM是等腰直角三角形;
∵∠PAN=∠NDP=45°,
∴点A,D,N,P四点共圆,
∴∠APN+∠ADN=180°,
∵∠ADN=90°,
∴∠APN=90°,
∵∠PAN=45°,
∴△APN为等腰直角三角形.
点评 本题考查四边形综合题、等腰直角三角形判定、四点共圆、相似三角形的判定和性质等知识,解题的关键是判断出△AMC∽△AQD,判断四点共圆是解本题的难点.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com