
 用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成图2所示的Rt△BCE.若Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB=a,BC=b,b满足a+b=m-1,ab=m+1,则点D到CM的距离为( )
用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成图2所示的Rt△BCE.若Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB=a,BC=b,b满足a+b=m-1,ab=m+1,则点D到CM的距离为( )| A. | $2\sqrt{2}$ | B. | 4 | C. | 2 | D. | $\sqrt{2}$ |
分析 若是等腰直角三角形的话,b=2a,这样代入a+b=m-1,ab=m+1,求出m的值,再根据等腰直角三角形的性质得到点D到CM的距离.
解答 解:因为Rt△BCE是等腰直角三角形,M为AD的中点,所以b=2a.
∵a+b=m-1,
∴a+2a=m-1,
∴a=$\frac{m-1}{3}$,
∴$\frac{m-1}{3}$•$\frac{2(m-1)}{3}$=m+1,
m=-$\frac{1}{2}$(舍去)或m=7,
∴a=$\frac{m-1}{3}$=2,
∴点D到CM的距离为2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$.
故选:D.
点评 本题考查图形的剪拼,根据等腰直角三角形找到矩形的长和宽的关系,以及矩形的性质等知识点求解.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
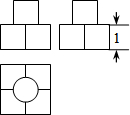 如图是某几何体的三视图,其中主视图和左视图是由若干个大小相等的正方形构成的.根据图中所标的尺寸,该几何体的表面积是16+π(不取近似值).
如图是某几何体的三视图,其中主视图和左视图是由若干个大小相等的正方形构成的.根据图中所标的尺寸,该几何体的表面积是16+π(不取近似值).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
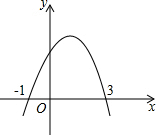 如图,抛物线y=ax2+bx+c交x轴于(-1,0)、(3,0)两点,则下列判断中,正确的是( )
如图,抛物线y=ax2+bx+c交x轴于(-1,0)、(3,0)两点,则下列判断中,正确的是( )| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A、B(点A在B的左侧),与y轴交于点C,若点F是直线BC上方的抛物线上一动点,是否存在点F,使△BCF的面积最大?若存在,求出定F的坐标;若不存在,请说明理由.
如图,已知抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A、B(点A在B的左侧),与y轴交于点C,若点F是直线BC上方的抛物线上一动点,是否存在点F,使△BCF的面积最大?若存在,求出定F的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC中,∠BAC=90°,AB=AC,D为AC的中点,CF⊥BD,AE⊥AF
如图,Rt△ABC中,∠BAC=90°,AB=AC,D为AC的中点,CF⊥BD,AE⊥AF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 周末,东东一家三口人开车去距家15km的二克山公园游玩,行驶10min后,接到爷爷奶奶的电话,也要一同前往,于是妈妈下午步行前往,东东和爸爸开车按原路返回接爷爷奶奶,接到爷爷奶奶后,开车前往公园,在距离公园3.75km处追上妈妈并同车前往公园,若汽车速度始终保持不变,设汽车与家相距y1(单位:km),妈妈与家相距y2(单位:km),汽车离开家的时间为x(单位:min),y1、y2与x之间的函数图象如图所示,结合图象解答下列问题:
周末,东东一家三口人开车去距家15km的二克山公园游玩,行驶10min后,接到爷爷奶奶的电话,也要一同前往,于是妈妈下午步行前往,东东和爸爸开车按原路返回接爷爷奶奶,接到爷爷奶奶后,开车前往公园,在距离公园3.75km处追上妈妈并同车前往公园,若汽车速度始终保持不变,设汽车与家相距y1(单位:km),妈妈与家相距y2(单位:km),汽车离开家的时间为x(单位:min),y1、y2与x之间的函数图象如图所示,结合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com