
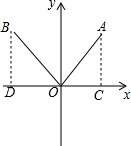
 如图,OA=10,OB=6,∠xOA=60°,∠xOB=135°,求A,B两点坐标.
如图,OA=10,OB=6,∠xOA=60°,∠xOB=135°,求A,B两点坐标.| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 2 |
 ,
,| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| 2 |


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
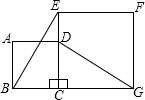 如图所示,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE,DG.
如图所示,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE,DG.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、当a=0,1,2,3时,代数式的值为质数 |
| B、不能肯定a为任何自然数时,代数式的值都是质数 |
| C、当a=11时,代数式的值为合数 |
| D、当a为任意实数时,代数式的值不是质数就是合数 |
查看答案和解析>>
科目:初中数学 来源: 题型:
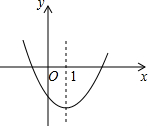 二次函数y=ax2+bx+c图象如图,下列正确的个数为( )
二次函数y=ax2+bx+c图象如图,下列正确的个数为( )| A、2 | B、3 | C、4 | D、5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,将直线y=x沿x轴负方向平移4个单位后,恰好与双曲线y=
如图,将直线y=x沿x轴负方向平移4个单位后,恰好与双曲线y=| m |
| x |
| n |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com