

分析 (1)由捐款15元的人数除以占的百分比,即可确定出该班学生的总人数;求出“捐款5元”的学生所占的百分比,再乘以360°即可得到“捐款5元”所在扇形的圆心角的度数;
(2)求出捐款10元、25元的人数,补全条形统计图,根据众数是一组数据中出现次数最多的数据求解即可;
(3)根据加权平均数的求解方法列式计算即可得解.
解答 解:(1)该班学生的总人数为:$\frac{14}{28%}$=50(名),
“捐款5元”所在扇形的圆心角的度数为:$\frac{10}{50}×360°=72°$;
(2)捐款10元的人数为:50×32%=16(人),
捐款25元的人数为:50-(10+16+14+6)=4(人),
画条形图,如图所示: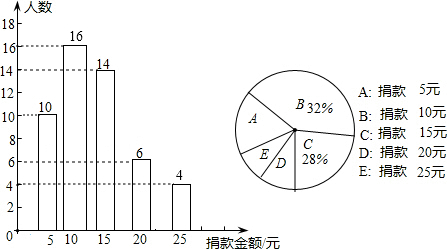
10元出现的次数最多,所以捐款金额的众数为:10元;
(3)该班平均每人捐款:$\frac{10×5+16×10+14×15+6×20+4×25}{50}=12.8$(元).
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-5)^{2}}$=-5 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{9}$=±3 | D. | $\root{3}{-27}$=-3 |
查看答案和解析>>
科目:初中数学 来源:2017届广东省广州市九年级下学期3月月考数学试卷(解析版) 题型:判断题
类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做等邻边四边形.
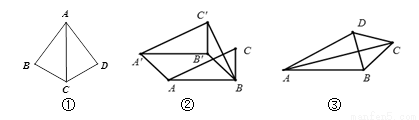
(1)如图①,四边形ABCD中,AC平分∠BAD,∠B=∠D. 求证:四边形ABCD为等邻边四边形.
(2)如图②,Rt△ABC中,∠ABC=90°,AB=2,BC=1,将△ABC沿∠ABC的平分线BB′的方向平移,得到△A′B′C′,连接AA′、BC′,若平移后的四边形ABC′A′是等邻边四边形,且满足BC′=AB,求平移的距离.
(3)如图③,在等邻边四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC和BD为四边形对角线,△BCD为等边三角形,试探究AC和AB的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com