练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．已知$\frac{1+x}{1-x}$=$\frac{1-y}{1+y}$，求（2+x）（2+y）+x2的值．

    分析 已知等式去分母整理得到x=-y，代入原式后利用平方差公式计算即可得到结果．

    解答 解：由$\frac{1+x}{1-x}$=$\frac{1-y}{1+y}$，得到（1+x）（1+y）=（1-x）（1-y），即1+x+y+xy=1-x-y+xy，
    整理得：x=-y，
    则原式=（2+x）（2-x）+x2=4-x2+x2=4．

    点评 此题考查了整式的混合运算-化简求值，以及分式的混合运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．计算，其中第（2）题用计算器计算．
    （1）（-2）2-$\sqrt{\frac{9}{4}}$+（-3）0；
    （2）$\frac{1}{4}$×$\root{3}{15}$-2×$\sqrt{5}$+$\frac{1}{6}$（精确到十分位）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：
    （1）$\frac{a}{a-2}$÷$\frac{a}{（2-a）（a+3）}$；
    （2）$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-6x+9}$$÷\frac{x+y}{2x-6}$；
    （3）$\frac{2y}{x-1}$+$\frac{3y}{1-x}$-$\frac{y}{1-x}$；
    （4）$\frac{y}{{x}^{2}-xy}$$÷\frac{x}{{y}^{2}-xy}$；
    （5）（$\sqrt{2}-\sqrt{3}$）0-（$\frac{1}{2}$）-1+$\sqrt{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

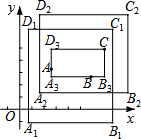    4．在平面直角坐标系xOy中，对于任意三点A，B，C，给出如下定义：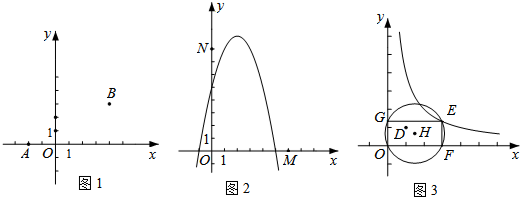
    若矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的外延矩形．点A，B，C的所有外延矩形中，面积最小的矩形称为点A，B，C的最佳外延矩形．例如，图1中的矩形A1B1C1D1，A2B2C2D2，A3B3CD3都是点A，B，C的外延矩形，矩形A3B3CD3是点A，B，C的最佳外延矩形．
    （1）如图1，已知A（-2，0），B（4，3），C（0，t）．
    ①若t=2，则点A，B，C的最佳外延矩形的面积为18；
    ②若点A，B，C的最佳外延矩形的面积为24，则t的值为4或-1；
    （2）如图2，已知点M（6，0），N（0，8）．P（x，y）是抛物线y=-x2+4x+5上一点，求点M，N，P的最佳外延矩形面积的最小值，以及此时点P的横坐标x的取值范围；
    （3）如图3，已知点D（1，1）．E（m，n）是函数y=$\frac{4}{x}$（x＞0）的图象上一点，矩形OFEG是点O，D，E的一个面积最小的最佳外延矩形，⊙H是矩形OFEG的外接圆，请直接写出⊙H的半径r的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．在面积为60的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F．若AB=10，BC=12，则CE-CF的值为（　　）
    A．2+$\sqrt{3}$B．22+11$\sqrt{3}$C．2-$\sqrt{3}$或22-11$\sqrt{3}$D．22-11$\sqrt{3}$或22+11$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．为了解某市九年级学生学业考试体育成绩，现从中随机抽取部分学生的体育成绩进行分段统计如下：
    学业考试体育成绩（分数段）统计表
    分数段人数（人）频率
    A480.2
    Ba0.25
    C840.35
    D36b
    E120.05
    根据上面提供的信息，回答下列问题：分数段为：（A：50分；B：49-45分；C：44-40分；D：39-30分；E：29-0分）
    （1）在统计表中，a的值为60，b的值为0.15，并将统计图补充完整（温馨提示：作图时别忘了用0.5毫米及以上的黑色签字笔涂黑）；
    （2）甲同学说：“我的体育成绩是此次抽样调查所得数据的中位数．”请问：甲同学的体育成绩应在什么分数段内？C（填相应分数段的字母）
    （3）如果把成绩在40分以上（含40分）定为优秀，那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

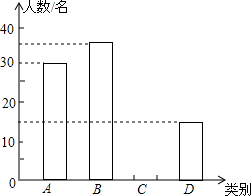    8．由于各地雾霾天气越来越严重，2015年春节前夕，某校团委向全校2000多名学生发出“减少空气污染，少放烟花爆竹”倡议书，并围绕“A类：不放烟花爆竹；B类：少放烟花爆竹；C类：不会减少烟花爆竹数量；D类：使用电子鞭炮”四个选项对100名学生进行问卷调查，并将调查结果绘制成如下两幅统计图表（不完整），请根据图表，回答下列问题：
    类别频数频率
    A30b
    B350.35
    C200.20
    Da0.15
    合计1001.00
    （1）表格中a=15，b=0.3，并补全条形统计图；
    （2）如果绘制扇形统计图，请求出C类所占的圆心角的度数；
    （3）根据抽样结果，请估计全校“使用电子鞭炮”的学生有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．甲乙两班的学生人数相等，参加了同一次数学测试，两班的平均分都是89分，方差分别为S甲2=2.56，
    S乙2=1.92，那么成绩比较整齐的班级是（　　）
    A．甲班B．乙班C．两班一样整齐D．无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．解方程：$\frac{18}{{x}^{2}-x}$=x2-x-3．

    查看答案和解析>>

    同步练习册答案