

分析 (1)根据旋转的性质可知:∠A1C1B=30°,再由等边对等角得∠BC1C=30°,则∠CC1A1=60°;
(2)由△ABC≌△A1BC1得比例式,证明△ABA1∽△CBC1,根据面积比等于相似比的平方求出△CBC1的面积;
(3)作辅助线,当点P在D处时BP最小,则BP1最小,EP1最小;当点P在点C处时,BP最大,则BP1最大,EP1最大,代入计算.
解答 解:(1)如图1,由旋转得:∠A1C1B=∠C=30°,BC=BC1,
∴∠C=∠BC1C=30°,
∴∠CC1A1=60°,
故答案为:60°;
(2)如图2,∵△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴$\frac{BA}{BC}=\frac{B{A}_{1}}{B{C}_{1}}$,
∵∠ABA1=∠CBC1,
∴△ABA1∽△CBC1,
∴$\frac{{S}_{△AB{A}_{1}}}{{S}_{△CB{C}_{1}}}$=$(\frac{AB}{AC})^{2}$=$(\frac{6}{11})^{2}$=$\frac{36}{121}$,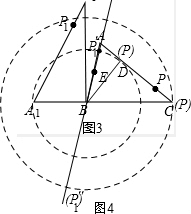
∵${S}_{△AB{A}_{1}}$=24,
∴${S}_{△CB{C}_{1}}$=$\frac{242}{3}$;
(3)如图4,过点B作BD⊥AC,D为垂足,
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin30°=5.5,
以B为圆心,BD为半径画圆交AB于P1′,BP1有最小值BP1′.
∴EP1的最小值为5.5-3=2.5,
以B为圆心,BC为半径画圆交AB的延长线于P1″,BP1有最大值BP1″.
此时EP1的最大值为11+3=14,
∴线段EP1的最大值与最小值的差为14-2.5=11.5.
点评 本题是三角形旋转的综合题,考查了三角形旋转的性质:旋转前后的两个图形全等;考查了全等三角形和相似三角形的对应边的关系,本题利用两三角形全等的对应边相等,列比例式证明另外两三角形相似,这一证明思路值得借鉴.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
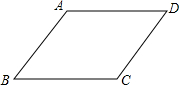 如图,平行四边形ABCD中,∠B=60°,AB=8cm,AD=10cm,点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P,Q运动的速度都为每秒1cm,那么当运动时间t=7秒时,四边形ABPQ是直角梯形.
如图,平行四边形ABCD中,∠B=60°,AB=8cm,AD=10cm,点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P,Q运动的速度都为每秒1cm,那么当运动时间t=7秒时,四边形ABPQ是直角梯形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于x的函数y=ax2-2abx+ab2-1,直线y=-ax+3与y轴交于点A,与x轴的正半轴交于点P,点B的纵坐标为3,且AP⊥BP,AP=BP.
已知关于x的函数y=ax2-2abx+ab2-1,直线y=-ax+3与y轴交于点A,与x轴的正半轴交于点P,点B的纵坐标为3,且AP⊥BP,AP=BP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com