解:(1)(

+
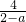
)•
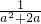
=(

-

)•

=

•

=

,
当a=1时,原式=1;
(2)(x
2+y
2)
2-(x
2+y
2)-12=0,
设x
2+y
2=a,则有a
2-a-12=0,
因式分解得:(a-4)(a+3)=0,
解得:a
1=4,a
2=-3,
∵x
2+y
2>0,即a>0,
∴a=-3不合题意,舍去,
则x
2+y
2=a=4.
分析:(1)将原式括号中的第二项分母提取-1变形为a-2,然后利用同分母分式的减法法则化简,分子再利用平方差公式分解因式,括号外边的分式分母提取a分解因式,约分可得出最简结果,然后选择a不为2,-2及0的值,比如a=1,将a=1代入化简后的式子中计算,即可得到原式的值;
(2)设a=x
2+y
2,将原方程化为关于a的一元二次方程,利用分解因式法求出方程的解得到a的值,根据x
2+y
2大于等于0,得到a大于等于0,将不合题意的a的值舍去,得到满足题意a的值,即为x
2+y
2的值.
点评:此题考查了分式的化简求值,以及利用换元法求方程的解,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,本题第二小题利用换元法求方程解时,注意x
2+y
2≥0.

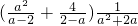 ,再选你最喜欢的a值代入求值.
,再选你最喜欢的a值代入求值. +
+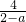 )•
)•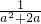
 -
- )•
)•
 •
•
 ,
,

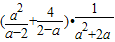 ,再选你最喜欢的a值代入求值.
,再选你最喜欢的a值代入求值.