

 =t,试用t表示EF的长;
=t,试用t表示EF的长; AD•AF=
AD•AF= x,S3=
x,S3= BC•BF=
BC•BF= ×2×(3﹣x)=3﹣x,
×2×(3﹣x)=3﹣x,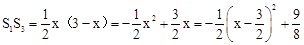 (0<x<3)。
(0<x<3)。 时,S1S3的最大值为
时,S1S3的最大值为 。
。
 =t,∴AF=tFB。
=t,∴AF=tFB。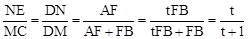 。∴NE=
。∴NE= ,
, 。
。 。∴AF=tFB=
。∴AF=tFB= 。
。 AD•AF=
AD•AF= ×
× =
= ,S3=
,S3= BC•FB=
BC•FB= ×2×
×2× =
= ,
, AB•FE=
AB•FE= ×3×
×3× =
=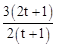 。
。 ,S22=
,S22= 。
。 =4×
=4× ,即4t2﹣4t+1=0,解得t=
,即4t2﹣4t+1=0,解得t= 。
。 时,S22=4S1S3。
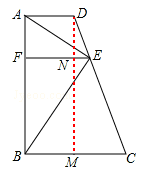
时,S22=4S1S3。 =t,可知AF=tFB,再由△DNE∽△DMC 和BM=MC=AD=1可得出
=t,可知AF=tFB,再由△DNE∽△DMC 和BM=MC=AD=1可得出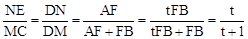 ,所以NE=
,所以NE= ,根据EF=FN+NE即可得出结论。
,根据EF=FN+NE即可得出结论。 ,故可得出AF=tFB=
,故可得出AF=tFB= ,根据三角形的面积公式可用t表示出S1,S3,S2,由s22=4S1S3.即可得出t的值。
,根据三角形的面积公式可用t表示出S1,S3,S2,由s22=4S1S3.即可得出t的值。

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源:不详 题型:解答题

 (180°- ) =45°。 ∠BDM=45°(同理)。
(180°- ) =45°。 ∠BDM=45°(同理)。 ,
,查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.1:14 | B.3:14 | C.1:16 | D.3:16 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 与
与 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com