A
分析:根据平行四边形的判定得出平行四边形ABCD,推出AB=CD,AD=BC,根据平行线的性质推出∠ADB=∠CBD,∠CDB=∠ABD,∠AEF=∠CFB,根据全等三角形的判定证出即可.
解答:①△ADB≌△CBD,
理由是:∵AB∥CD,AD∥BC,
∴∠ADB=∠CBD,∠CDB=∠ABD,
∵BD=BD,
∴△ADB≌△CBD.(ASA).
②△ADE≌△CBF,
理由是:∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴AD=BC,CD=AB,
∵CF∥AE,
∴∠AEF=∠CFB,
∵∠ADB=∠CBD,
∴△ADE≌△CBF(AAS).
∴DE=BF,
∵BD=BD,
∴DF=BE,
∵AB=CD,∠ABD=∠CDB,
∴③△DCF≌△BAE,
∴共3对.
故选A.
点评:本题综合考查了运用平行线的性质、全等三角形的性质和判定、平行四边形的性质和判定进行推理,综合性较强,培养了学生分析问题和解决问题的能力.

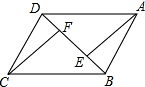 如图,AB∥CD,BC∥AD,AE∥CF,则图中全等三角形有
如图,AB∥CD,BC∥AD,AE∥CF,则图中全等三角形有
