Question

如图①，AB是⊙O的直径，AC是弦，直线EF和⊙O相切于点C，AD⊥EF，垂足为D。
【小题1】求证：∠DAC＝∠BAC；
【小题2】若把直线EF向上平行移动，如图②，EF交⊙O于G、C两点，若题中的其它条件不变，猜想：此时与∠DAC相等的角是哪一个？并证明你的结论。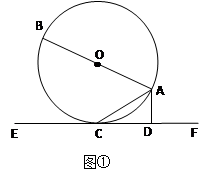

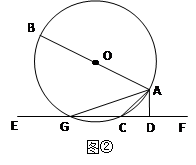
Answer 1

【小题1】连结OC，得OC∥AD。
【小题2】连结BG，得∠ACD＝∠B。

解析（1）连OC，构建平行线OC∥AD．然后由两直线平行，内错角相等推知∠OCA=∠DAC，再根据等腰三角形OAC两个底角相等的性质知，∠BAC=∠OCA，所以根据等量代换易证明：∠DAC=∠BAC；
（2）根据（2）的思路，可以直接写出答案．
证明：（1）连OC，
则OC=OA，
∴∠BAC=∠OCA （1分）
∵EF切⊙O于C，
∴OC⊥EF （2分）
∵AD⊥EF，
∴OC∥AD （3分）
∴∠OCA=∠DAC （4分）
∴∠DAC=∠BAC （5分）
(2）∠BAG=∠DAC，理由如下：
连接BC，
∵AB为⊙O的直径，
∴∠BCA=90°，∠B+∠BAC=90°，
∵∠AGD+∠GAD=90°，
又∵∠B=∠AGD，
∴∠BAC=∠GAD；
即∠BAG+∠GAC=∠GAC+∠DAC，
∴∠BAG=∠DAC． （12分）