Question

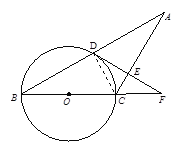
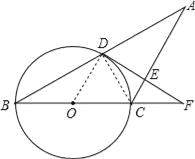
【题目】已知：如图，△ABC中，AC=BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于点E，交BC的延长线于点F．

求证：

（1）AD=BD；

（2）DF是⊙O的切线．

Answer 1

【答案】（1）证法一：连结CD，

∵BC为⊙O的直径

∴CD⊥AB

　　　 ∵AC＝BC

　　　 ∴AD＝BD．

证法二：连结CD，

　∵BC为⊙O的直径

∴∠ADC＝∠BDC＝90°

∵AC＝BC，CD＝CD

∴△ACD≌△BCD

∴AD＝BD

（2）证法一：连结OD，

　∵AD＝BD，OB＝OC

　　∴OD∥AC

　　∵DE⊥AC

∴DF⊥OD

　　∴DF是⊙O的切线．

证法二：连结OD，

　　　　∵OB=OD

　　　　∴∠BDO＝∠B

　　　　∵∠B＝∠A

　　　　∴∠BDO=∠A

　　　　∵∠A+∠ADE＝90°

　　　　∴∠BDO＋∠ADE＝90°

　　　　∴∠ODF=90°

　　　　∴DF是⊙O的切线．

【解析】试题分析：（1）由于AC=AB，如果连接CD，那么只要证明出CD⊥AB，根据等腰三角形三线合一的特点，我们就可以得出AD=BD，由于BC是圆的直径，那么CD⊥AB，由此可证得．

（2）连接OD，再证明OD⊥DE即可．

试题解析：（1）连接CD，

∵BC为⊙O的直径，

∴CD⊥AB．

∵AC=BC，

∴AD=BD．

（2）连接OD；

∵AD=BD，OB=OC，

∴OD是△BCA的中位线，

∴OD∥AC．

∵DE⊥AC，

∴DF⊥OD．

∵OD为半径，

∴DF是⊙O的切线．