练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图是由四个小正方体叠成的一个几何体，它的左视图是（ ）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省2018届九年级数学上期末复习检测数学试卷 题型：解答题

    如图，在平面直角坐标系中，二次函数的图象与x轴交于A、B两点，B点的坐标为(3，0)，与y轴交于点C（0，－3），点P是直线BC下方抛物线上的一个动点．

    （1）求二次函数解析式；

    （2）连接PO，PC，并将△POC沿y轴对折，得到四边形.是否存在点P，使四边形为菱形？若存在，求出此时点P的坐标；若不存在，请说明理由；

    （3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型：单选题

    在平面直角坐标系中，点A（﹣3，2），B（3，5），C（x，y），若AC∥x轴，则线段BC的最小值及此时点C的坐标分别为（   ）

    A. 6，（﹣3，5） B. 10，（3，﹣5） C. 1，（3，4） D. 3，（3，2）

    查看答案和解析>>

    科目：初中数学 来源：四川省达州市2018届中考二模试卷数学试卷 题型：填空题

    ⊙M的圆心在一次函数y=x+2图象上，半径为1．当⊙M与y轴相切时，点M的坐标为_____．

    查看答案和解析>>

    科目：初中数学 来源：四川省达州市2018届中考二模试卷数学试卷 题型：单选题

    已知抛物线c：y=x2+2x﹣3，将抛物线c平移得到抛物线c′，如果两条抛物线，关于直线x=1对称，那么下列说法正确的是（　　）

    A. 将抛物线c沿x轴向右平移个单位得到抛物线c′ B. 将抛物线c沿x轴向右平移4个单位得到抛物线c′

    C. 将抛物线c沿x轴向右平移个单位得到抛物线c′ D. 将抛物线c沿x轴向右平移6个单位得到抛物线c′

    查看答案和解析>>

    科目：初中数学 来源：福建省泉州市片区2018年初二年下学期数学期中考试 题型：解答题

    济宁市“五城同创”活动中，一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天，甲工程队单独工作30天后，乙工程队参与合做，两队又共同工作了36天完成.

    （1）求乙工程队单独完成这项工作需要多少天？

    （2）因工期的需要，将此项工程分成两部分，甲做其中一部分用了x天完成，乙做另一部分用了y天完成，其中x、y均为正整数，且x<46，y<52，求甲、乙两队各做了多少天？

    查看答案和解析>>

    科目：初中数学 来源：福建省泉州市片区2018年初二年下学期数学期中考试 题型：填空题

    甲、乙两车分别从M、N两地相向而行，甲车出发1小时后乙车才出发，并以各自速度匀速行驶，甲车出发3小时两车相遇，相遇后两车仍按原速度原方向各自行驶．如图折线A-B-C-D表示甲、乙两车之间的距离S(千米) 与甲车出发时间(小时)之间的函数图象．则：

    ①M、N两地之间的距离为________________千米；

    ②当时，__________________小时．

    查看答案和解析>>

    科目：初中数学 来源：贵州省黔南州2018届中考数学二模试卷 题型：解答题

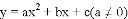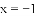
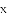
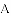
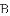
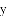
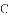
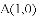
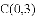
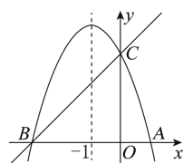
    如图，已知抛物线的对称轴为直线，且抛物线与轴交于、两点，与轴交于点，其中，.

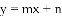
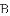
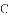
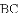
    （1）若直线经过、两点，求直线和抛物线的解析式；

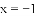
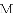
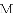
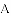
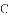
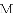
    （2）在抛物线的对称轴上找一点，使点到点的距离与到点的距离之和最小，求出点的坐标；

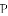
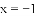
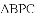
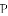
    （3）设点为抛物线的对称轴上的一个动点，求使为直角三角形的点的坐标.

    查看答案和解析>>

    科目：初中数学 来源：山东省济南市历城区2019届九年级上学期期中考试数学试卷 题型：单选题

    如图，在平面直角坐标系中，函数 y ? kx 与 y ? ?的图象交于 A、B 两点，过 A 作 y 轴的垂线，交函数的图象于点 C，连接 BC，则△ABC 的面积为（ ）

    A. 2 B. 4 C. 6 D. 8

    查看答案和解析>>

    同步练习册答案