
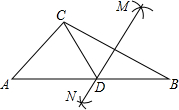
 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图:| 1 |
| 2 |
科目:初中数学 来源: 题型:
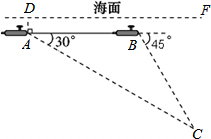 如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:
如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
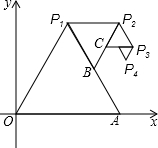 如图,以O(0,0)、A(2,0)为顶点作正△OAP1,以点P1和线段P1A的中点B为顶点作正△P1BP2,再以点P2和线段P2B的中点C为顶点作△P2CP3,…,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是
如图,以O(0,0)、A(2,0)为顶点作正△OAP1,以点P1和线段P1A的中点B为顶点作正△P1BP2,再以点P2和线段P2B的中点C为顶点作△P2CP3,…,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是查看答案和解析>>
科目:初中数学 来源: 题型:
 在一次“寻宝”游戏中,“寻宝”人找到了如图所标示的两个标志点A(2,3),B(4,1),A,B两点到“宝藏”点的距离都相等,则“宝藏”点的可能坐标是
在一次“寻宝”游戏中,“寻宝”人找到了如图所标示的两个标志点A(2,3),B(4,1),A,B两点到“宝藏”点的距离都相等,则“宝藏”点的可能坐标是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com