
| A. | 3 | B. | 5 | C. | 6 | D. | 7 |
分析 设DP=x,根据已知可以分三种情况:①当点P在线段BD上时;②当点P在线段BD的右侧时;③当点P在线段BD的左侧时;分别得出比例式得出方程,解方程求出x的值,即可得出结果.
解答 解:∵AB⊥DB,CD⊥DB,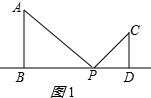
∴∠D=∠B=90°,
设DP=x,分三种情况:
①当点P在线段BD上时,
当PD:AB=CD:PB时,△PDC∽△ABP,
∴$\frac{x}{6}=\frac{x}{14-x}$,解得:DP=2或12,
当PD:PB=CD:AB时,△PCD∽△PAB,
∴$\frac{x}{14-x}=\frac{4}{6}$,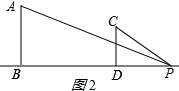
解得:DP=5.6;
②当点P在线段BD的右侧,如图1所示:
当$\frac{PD}{PB}=\frac{CD}{AB}$时,△PCD∽△PAB,
即$\frac{x}{x+14}=\frac{4}{6}$,
解得:x=28;
当$\frac{PD}{AB}=\frac{CD}{PB}$时,△PCD∽△APB,
即$\frac{x}{6}=\frac{4}{x+14}$,
解得:x=-7±$\sqrt{73}$(负值舍去),
∴PD=-7+$\sqrt{73}$;
③当点P在线段BD的左侧时,如图2所示: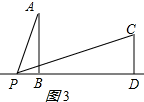
当$\frac{PB}{CD}=\frac{AB}{PD}$时,△PCD∽△APB,
即$\frac{x}{14-x}=\frac{6}{x}$,
解得:x=7±$\sqrt{73}$(负值舍去),
∴PD=7+$\sqrt{73}$;
综上所述:当DP=5.6或2或12或28或-7+$\sqrt{73}$或7+$\sqrt{73}$时,△ABP与△CDP相似,即这样的点P的个数有6个;
故选:C.
点评 此题考查了相似三角形的判定方法;熟练掌握相似三角形的判定方法,分三种情况讨论得出比例式是解决问题的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:解答题
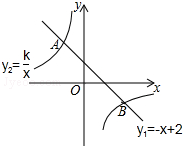 如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,点B的坐标为(2m,-m).
如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,点B的坐标为(2m,-m).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年份 | 2008 | 2009 | 2010 | 1211 | 2012 |
| 产值/万元 | 80 | 90 | 110 | 130 | 155 |
| A. | 2009年 | B. | 2011年 | C. | 2010年 | D. | 2012年 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
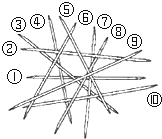 挑游戏棒是一种好玩的游戏,游戏规则:当一根棒条没有被其它棒条压着时,就可以把它往上拿走.如图中,按照这一规则,第1次应拿走⑨号棒,第2次应拿走⑤号棒,…,则第6次应拿走⑦.
挑游戏棒是一种好玩的游戏,游戏规则:当一根棒条没有被其它棒条压着时,就可以把它往上拿走.如图中,按照这一规则,第1次应拿走⑨号棒,第2次应拿走⑤号棒,…,则第6次应拿走⑦.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com