
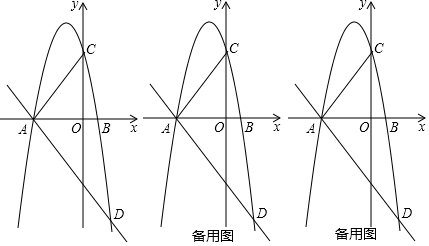
���� ��1�����ݶ��κ����Ľ���ʽȷ����A��B�����꣬�������ֱ��AD�Ľ���ʽ�����������D�����꣬��D��������������߽���ʽȷ��a��ֵ��
��2������ϵ�����õ�ֱ��AC�Ľ���ʽΪy=$\sqrt{3}$x+3$\sqrt{3}$��������֪�����õ���CP��AC���õ�ֱ��CP�Ľ���ʽΪ��y=-$\frac{\sqrt{3}}{3}$x+3$\sqrt{3}$��������֪�����õ���AP��AC���õ�ֱ��AP�Ľ���ʽΪ��y=-$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$���ⷽ���鼴�ɵõ����ۣ�
��3����DM��x�ύ��������M����DN��x����N����EF��DM��F���������еĶ������Q���˶�ʱ��t=BE+EFʱ��t��С���ɣ�
��� �⣺��1����y=a��x+3����x-1����
���A��������-3��0������B����������1��0����
��ֱ��y=-$\sqrt{3}$x+b������A��
��b=-3$\sqrt{3}$��
��y=-$\sqrt{3}$x-3$\sqrt{3}$��
��x=2ʱ��y=-5$\sqrt{3}$��
���D��������2��-5$\sqrt{3}$����
�ߵ�D���������ϣ�
��a��2+3����2-1��=-5$\sqrt{3}$��
��ã�a=-$\sqrt{3}$��
�������ߵĽ���ʽΪy=-$\sqrt{3}$��x+3����x-1��=-$\sqrt{3}$x2-2$\sqrt{3}$x+3$\sqrt{3}$��
��2����A��������-3��0����C��0��3$\sqrt{3}$����
��ֱ��AC�Ľ���ʽΪ��y=$\sqrt{3}$x+3$\sqrt{3}$��
�١ߡ�ACP����ACΪֱ�DZߵ�ֱ�������Σ�
��CP��AC��
����ֱ��CP�Ľ���ʽΪ��y=-$\frac{\sqrt{3}}{3}$x+m��
��C��0��3$\sqrt{3}$�������m=3$\sqrt{3}$��
��ֱ��CP�Ľ���ʽΪ��y=-$\frac{\sqrt{3}}{3}$x+3$\sqrt{3}$��
��$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x+3\sqrt{3}}\\{y=-\sqrt{3}{x}^{2}-2\sqrt{3}x+3\sqrt{3}}\end{array}\right.$��$\left\{\begin{array}{l}{x=-\frac{5}{3}}\\{y=\frac{32\sqrt{3}}{9}}\end{array}\right.$��$\left\{\begin{array}{l}{x=0}\\{y=3\sqrt{3}}\end{array}\right.$���������⣬��ȥ����
��P��-$\frac{5}{3}$��$\frac{32\sqrt{3}}{9}$����
�ڡߡ�ACP����ACΪֱ�DZߵ�ֱ�������Σ�
��AP��AC��
����ֱ��CP�Ľ���ʽΪ��y=-$\frac{\sqrt{3}}{3}$x+n��
��A��-3��0�������n=-$\sqrt{3}$��
��ֱ��AP�Ľ���ʽΪ��y=-$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$��
��y=-$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x-\sqrt{3}}\\{y=-\sqrt{3}{x}^{2}-2\sqrt{3}x+3\sqrt{3}}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=-2\sqrt{3}}\end{array}\right.$��$\left\{\begin{array}{l}{x=-\frac{4}{3}}\\{y=-\frac{13\sqrt{3}}{9}}\end{array}\right.$���������⣬��ȥ����
��P��3��-2$\sqrt{3}$����
������������P��������-$\frac{5}{3}$��$\frac{32\sqrt{3}}{9}$����3��-2$\sqrt{3}$����
��3����ͼ2�У���DM��x�ύ��������M����DN��x����N����EF��DM��F��
��tan��DAN=$\frac{DN}{AN}$=$\frac{5\sqrt{3}}{5}$=$\sqrt{3}$��
���DAN=60�㣬
���EDF=60�㣬
��DE=$\frac{EF}{sin��EDF}$=$\frac{2\sqrt{3}}{3}$EF��
��Q���˶�ʱ��t=$\frac{BE}{1}$+$\frac{DE}{\frac{2\sqrt{3}}{3}}$=BE+EF��
�൱BE��EF����ʱ��t��С��
��BE��DM����ʱ��E���꣨1��-4$\sqrt{3}$����
���� ���⿼����Ƕ��κ���֪ʶ���ۺ����ã����ն��κ��������ʡ����κ����Ľ���ʽ�����������ε��ж����������ʶ����ǽ���Ĺؼ������ʱ��ע�������������ۣ������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2a+3b=5ab | B�� | a6��a3=a2 | C�� | ��a+b��2=a2+b2 | D�� | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 107 | B�� | 109 | C�� | 112 | D�� | 115 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+3��5 | B�� | x+3��6 | C�� | x+3��7 | D�� | x+3��5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com