
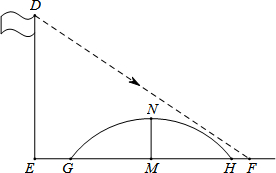
 (2013•深圳)如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
(2013•深圳)如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径. 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
 (2013•深圳)如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是( )
(2013•深圳)如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•深圳)如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是( )
(2013•深圳)如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•深圳)如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,廷长BC到E,使得CE=AD,连接DE.
(2013•深圳)如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,廷长BC到E,使得CE=AD,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
| 1 |
| 8 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com