
【题目】(1)叙述并证明三角形内角和定理(证明用图 1);
(2)如图 2 是七角星形,求∠A+∠B+∠C+∠D+∠E+∠F+∠G 的度数.

【答案】(1)见解析;(2) 180°
【解析】
(1)先写出已知、求证,再画图,然后证明.过点A作MN∥BC,利用MN∥BC,可得∠B=∠MAB,∠C=∠NAC,而∠MAB+∠NAC+∠BAC=180°,利用等量代换可证∠BAC+∠B+∠C=180°;
(2)先根据△外角的性质得出∠D+∠G=∠CMD,∠A+∠E=∠DMN,∠B+∠F=∠MNC,再由三角形内角和定理即可得出结论.
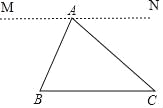
(1)证明:如图,过点 A 作直线 MN,使 MN∥BC,,
∵MN∥BC,
∴∠B=∠MAB,∠C=∠NAC(两直线平行,内错角相等)
∵∠MAB+∠NAC+∠BAC=180°(平角定义)
∴∠B+∠C+∠BAC=180°(等量代换)
∴∠BAC+∠B+∠C=180°.

(2)解:如图 2,
∵∠A+∠E=∠DME,∠G+∠D=∠ANG,∠C+∠F=∠BHC,
∵∠DME+∠ANG=∠BPH,
∴∠A+∠E+∠G+∠D=∠BPH,
∵∠B+∠BHC+∠BPH=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°.


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,点A的坐标为(﹣2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.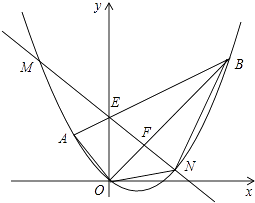
(1)求点E的坐标;
(2)求抛物线的函数解析式;
(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连接ON、BN,当点F在线段OB上运动时,求△BON面积的最大值,并求出此时点N的坐标;
(4)连接AN,当△BON面积最大时,在坐标平面内求使得△BOP与△OAN相似(点B、O、P分别与点O、A、N对应)的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了统计知识后,班主任王老师叫班长就本班同学的上学方式进行了一次调查统计,图1和图2是他通过收集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题: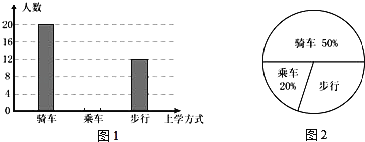
(1)在扇形统计图中,计算出“步行”部分所对应的圆心角的度数;
(2)求该班共有多少名学生;
(3)在图1中,将表示“乘车”的部分补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班男、女同学分别参加植树活动,要求男、女同学各植8行树,男同学植的树比女同学植的树多,如果每行都比预定的多植一棵树,那么男、女同学植树的数目都超过100棵;如果每行都比预定的少植一棵树,那么男、女同学植树的数目都达不到100棵,这样原来预定男同学植树______棵,女同学植树______棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装销售店到生产厂家选购A、B两种品牌的服装,若购进A品牌服装3套,B品牌服装4套,共需600元;若购进A品牌服装2套,B品牌服装3套,共需425元.
(1)求A、B两种品牌的服装每套进价分别为多少元?
(2)若A品牌服装每套售价为130元,B品牌服装每套售价为100元,根据市场的需求,现决定购进B品牌服装数量比A品牌服装数量的2倍还多3套.如果购进B品牌服装数量不多于39套,这样服装全部售出后,就能使获利总额不少于1335元,问共有几种进货方案?如何进货?(注:利润=售价-进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD. 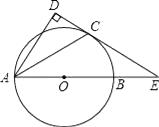
(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知CE⊥AB于点E,BD⊥AC于点D,BD与CE交于点O,且AO平分∠BAC.
(1)图中有多少对全等三角形?请你一一列举出来(不要求说明理由).
(2)小明说:欲说明BE=CD,可先说明△AOE≌△AOD得到AE=AD,再说明△ADB≌△AEC得到AB=AC,然后利用等式的性质即可得到BE=CD,请问他的说法正确吗?如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
(3)要得到BE=CD,你还有其他的思路吗?请仿照小明的说法具体说一说你的想法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,DE⊥BC,AB⊥BC,试说明:∠A=∠3.

解:因为DE⊥BC,AB⊥BC(已知),
所以∠DEC=∠ABC=90°(____________),
所以DE∥AB(____________________),
所以∠2=________(____________________),
∠1=________(____________________).
因为∠1=∠2(已知),
所以∠A=∠3(等量代换).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com