
(8分)已知以下基本事实:①对顶角相等;②一条直线截两条平行直线所得的同位角相等;③两条直线被第三条直线所截,若同位角相等,则这两条直线平行;④全等三角形的对应边、对应角分别相等.
1.(1)在利用以上基本事实作为依据来证明命题“两直线平行,内错角相等”时,必须要用的基本事实有 (填入序号即可);
2.(2)根据在(1)中的选择,结合所给图形,请你证明命题“两直线平行,内错角相等”.
已知:如图,_________________________________.
求证:_________________________________.
证明:
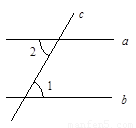
科目:初中数学 来源: 题型:
(8分)已知以下基本事实:①对顶角相等;②一条直线截两条平行直线所得的同位角相等;③两条直线被第三条直线所截,若同位角相等,则这两条直线平行;④全等三角形的对应边、对应角分别相等.
1.(1)在利用以上基本事实作为依据来证明命题“两直线平行,内错角相等”时,必须要用的基本事实有 (填入序号即可);
2.(2)根据在(1)中的选择,结合所给图形,请你证明命题“两直线平行,内错角相等”.
已知:如图,_________________________________.
求证:_________________________________.
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
(8分)已知以下基本事实:①对顶角相等;②一条直线截两条平行直线
所得的同位角相等;③两条直线被第三条直线所截,若同位角相等,则这两条直线
平行;④全等三角形的对应边、对应角分别相等.
(1)在利用以上基本事实作为依据来证明命题“两直线平行,内错角相等”时,必须要用的基本事实有 (填入序号即可);
(2)根据在(1)中的选择,结合所给图形,请你证明命题“两直线平行,内错角相等”.
已知:如图,_________________________________.
求证:_________________________________.
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011届上海市奉贤区4月中考数学模拟试卷 题型:解答题
(8分)已知以下基本事实:①对顶角相等;②一条直线截两条平行直线
所得的同位角相等;③两条直线 被第三条直线所截,若同位角相等,则这两条直线
被第三条直线所截,若同位角相等,则这两条直线
平行;④全等三角形的对应边、对应角分别相等.
(1)在利用以上基本事实作为依据来证明命题“两直线平行,内错角相等”时,必须要用的基本事实有 (填入序号即可);
(2)根据在(1)中的选择,结合所给图形,请你证明命题“两直线平行,内错角相等”.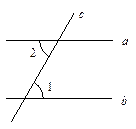
已知:如图,_________________________________.
求证:_________________________________.
证明:
查看答案和解析>>
科目:初中数学 来源:2010-2011学年上海市考数学模拟试卷 题型:解答题
(8分)已知以下基本事实:①对顶角相等;②一条直线截两条平行直线
所得的同位角相等;③两条直线被第三条直线所截,若同位角相等,则这两条直线
平行;④全等三角形的对应边、对应角分别相等.
(1)在利用以上基本事实作为依据来证明命题“两直线平行,内错角相等”时,必须要用的基本事实有 (填入序号即可);
(2)根据在(1)中的选择,结合所给图形,请你证明命题“两直线平行,内错角相等”.

已知:如图,_________________________________.
求证:_________________________________.
证明:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com