练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    (8分)如图，AB是半圆的直径，点O是圆心，点C是OA的中点，CD⊥OA交

    半圆于点D，点E是的中点，连接AE、OD，过点D作DP∥AE交BA的延长线于点P．

    (1)求∠AOD的度数；

    (2)求证：PD是半圆O的切线．

     

    （1）解：∵点C时OA的中点，∴OC=OA=OD

    ∵CD⊥OA，∴∠OCD=90°。

    在Rt△OCD中，cos∠COD=

    ∴∠COD=60°，即∠AOD=60°。

    （2）证明：连结OE，∵点E是的中点，

    ∴，

    ∴∠BOE=∠DOE=∠DOB=（180°-∠COD）=（180°-60°）=60°。

    ∵OA=OE，∴∠EAO=∠AEO，又∠EAO+∠AEO=∠EOB=60°

    ∴∠EAO=30°，

    ∴PD∥AE，

    ∴∠P=∠EAO=30°。

    由（1）知∠AOD=60°，∴∠PDO=180°-（∠P+∠POD）=180°-（30°+60°）=90°，

    ∴PD是半圆O的切线。

    解析:略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （11·漳州）（满分10分）如图，AB是⊙O的直径，，∠COD＝60°．

    （1）△AOC是等边三角形吗？请说明理由；
    （2）求证：OC∥BD．

    查看答案和解析>>

    科目：初中数学 来源：2010年高级中等学校招生全国统一考试数学卷（浙江杭州） 题型：解答题

    （本题满分10分）如图，AB是⊙O的直径， P为AB延长线上任意一点，C为半圆ACB的中点，PD切⊙O于点D，连结CD交AB于点E．

    求证：（1）PD=PE；
    （2）．

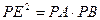    查看答案和解析>>

    科目：初中数学 来源：2010-2011学年山东省滨州市滨城区九年级第一学期期末测试数学卷 题型：解答题

    （本题满分l0分）
    如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交弧BC于D．

    【小题1】（1）请写出四个不同类型的正确结论；
    ①  _____________；②__________；③__________；④______．
    【小题2】（2）若BC=8，ED=2，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源：2013届江苏省宿迁市四校（桃洲、洪翔中学）九年级第二次联考数学试卷（带解析） 题型：解答题

    （本题10分）如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交于D.

    （1）请写出四个不同类型的正确结论；
    （2）若BC = 8，ED = 2，求⊙O的半径.

    查看答案和解析>>

    科目：初中数学 来源：2012届部分学校九年级下学期联考数学卷 题型：解答题

    （本题满分8分）如图，AB是⊙O的直径，AC、BC是弦，D，DE⊥AB于E，交BC于F. 已知AC=6，⊙O的半径是5.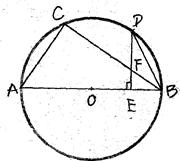

    【小题1】(1)求证：BC=2DE
    【小题2】(2)求tan∠CBD的值

    查看答案和解析>>

    同步练习册答案