[题目]直线y=﹣x与双曲线y=在同一坐标系中的大致位置是( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

【题目】直线y=﹣x与双曲线y=在同一坐标系中的大致位置是（　　）
A.
B.
C.
D.

【答案】D
【解析】解：∵直线y=﹣x中的k=﹣1＜0，
∴该直线经过第二、四象限；
∵双曲线y=中的k=1＞0，
∴该直线经过第一、三象限；
观察选项，D选项符合题意．
故选：D．
【考点精析】根据题目的已知条件，利用正比例函数的图象和性质和反比例函数的图象的相关知识可以得到问题的答案，需要掌握正比函数图直线，经过一定过原点．K正一三负二四，变化趋势记心间．K正左低右边高，同大同小向爬山．K负左高右边低，一大另小下山峦；反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，在正方形ABCD中，E是BC的中点，F是CD上一点，且CF=CD，求证：∠AEF=90°．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△OAB中，O为坐标原点，横、纵轴的单位长度相同，A、B的坐标分别为(8，6)，(16，0)，点P沿OA边从点O开始向终点A运动，速度每秒1个单位，点Q沿BO边从B点开始向终点O运动，速度每秒2个单位，如果P、Q同时出发，用t(秒)表示移动时间，当这两点中有一点到达自己的终点时，另一点也停止运动。求：

（1）几秒时PQ∥AB.

（2）设△OPQ的面积为y，求y与t的函数关系式.

（3）△OPQ与△OAB能否相似?若能，求出点P的坐标，若不能，试说明理由.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，点A的坐标是（10，0），点B的坐标为（8，0），点C、D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，求点C的坐标．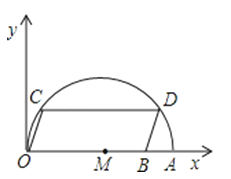

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”．图中点A表示﹣11，点B表示10，点C表示18，我们称点A和点C在数轴上相距29个长度单位．动点P从点A出发，以2单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速；同时，动点Q从点C出发，以1单位/秒的速度沿着数轴的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后也立刻恢复原速．设运动的时间为t秒．

问：（1）动点P从点A运动至C点需要多少时间？

（2）P、Q两点相遇时，求出相遇点M所对应的数是多少；

（3）求当t为何值时，P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】使得函数值为零的自变量的值称为函数的零点．例如，对于函数y＝x－1，令y＝0可得x＝1，我们就说1是函数y＝x－1的零点．

已知y＝x2－2mx－2(m＋3)(m为常数)．

(1)当m＝0时，求该函数的零点；

(2)证明：无论m取何值，该函数总有两个零点；

(3)设函数的两个零点分别为x1和x2，且，此时函数图象与x轴的交点分别为A，B(点A在点B左侧)，点M在直线y＝x－10上，当MA＋MB最小时，求直线AM的函数表达式．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在阳光体育活动时间，小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球，当时只有一副空球桌，他们只能选两人打第一场．
（1）如果确定小亮打第一场，再从其余三人中随机选取一人打第一场，求恰好选中大刚的概率；
（2）如果确定小亮做裁判，用“手心、手背”的方法决定其余三人哪两人打第一场．游戏规则是：三人同时伸“手心、手背”中的一种手势，如果恰好有两人伸出的手势相同，那么这两人上场，否则重新开始，这三人伸出“手心”或“手背”都是随机的，请用画树状图的方法求小莹和小芳打第一场的概率．

查看答案和解析>>

科目：初中数学 来源： 题型：