
 如图,点A为函数y=$\frac{9}{x}$(x>0)的图象上一点,连接OA,交函数y=$\frac{1}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积是( )
如图,点A为函数y=$\frac{9}{x}$(x>0)的图象上一点,连接OA,交函数y=$\frac{1}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积是( )| A. | $\frac{9}{2}$ | B. | 9 | C. | 6 | D. | 3 |
分析 作辅助线,根据反比例函数关系式得:S△AOD=$\frac{9}{2}$,S△BOE=$\frac{1}{2}$,再证明△BOE∽△AOD,由性质得OB与OA的比,由同高两三角形面积的比等于对应底边的比可以得出结论.
解答  解:过A作AD⊥x轴于D,过B作BE⊥x轴于E,
解:过A作AD⊥x轴于D,过B作BE⊥x轴于E,
∴BE∥AD,
∴△BOE∽△AOD,
∴$\frac{{S}_{△BOE}}{{S}_{△AOD}}$=$\frac{O{B}^{2}}{O{A}^{2}}$,
∵OA=AC,
∴OD=DC,
∴S△AOD=S△ADC=$\frac{1}{2}$S△AOC,
∵点A为函数y=$\frac{9}{x}$(x>0)的图象上一点,
∴S△AOD=$\frac{9}{2}$,
同理得:S△BOE=$\frac{1}{2}$,
∴$\frac{{S}_{△BOE}}{{S}_{△AOD}}$=$\frac{\frac{1}{2}}{\frac{9}{2}}$=$\frac{1}{9}$,
∴$\frac{OB}{OA}$=$\frac{1}{3}$,
∴$\frac{AB}{OA}$=$\frac{2}{3}$,
∴$\frac{{S}_{△ABC}}{{S}_{△AOC}}$=$\frac{2}{3}$,
∴S△ABC=$\frac{2×9}{3}$=6,
故选C.
点评 此题考查了反比例函数的几何意义,属于基础题,关键是掌握在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.


科目:初中数学 来源: 题型:填空题
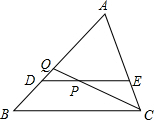 如图,DE∥BC,且过△ABC的重心,分别与AB、AC交于点D、E,点P是线段DE上一点,CP的延长线交AB于点Q,如果$\frac{DP}{DE}$=$\frac{1}{4}$,那么S△DPQ:S△CPE的值是1:15.
如图,DE∥BC,且过△ABC的重心,分别与AB、AC交于点D、E,点P是线段DE上一点,CP的延长线交AB于点Q,如果$\frac{DP}{DE}$=$\frac{1}{4}$,那么S△DPQ:S△CPE的值是1:15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)观察思考
(1)观察思考查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )| A. | x<-1或x>4 | B. | x<-1或0<x<4 | C. | -1<x<4 | D. | -1<x<0或x>4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小明从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了( )
如图,小明从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了( )| A. | 240m | B. | 230m | C. | 220m | D. | 200m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com