
【题目】如图,四边形ABCD,![]() ,
,![]() ,连接BD.
,连接BD.

(1)如图1,求证DB平分![]() ;
;
(2)如图2,连接AC,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,延长AD交BC的延长线于F,点E在边AB上,![]() ,连CE交BD于G,当
,连CE交BD于G,当![]() ,
,![]() 时,求BD的长.
时,求BD的长.
【答案】(1)见解析;(2)见解析;(3)7
【解析】
(1)过B作BE⊥AD于E,过B作BF⊥DC于F.根据四边形内角和为360°得到∠A+∠DCB=180°.再根据同角的补角相等得到∠A=∠FCB.即可证明△AEB≌△CFB,得到BE=BF,根据到角两边距离相等的点在角平分线上即可得到结论;
(2)如图2中,在BD截取DE=AD,连接AE,首先证明△ADE是等边三角形,只要证明△DAC≌△EAB(SAS),即可解决问题;
(3)如图3中,作EN∥DC交BD于N,在DF上截取DM=DC.想办法证明△CFM≌△EBN(AAS),△DGC≌△NGE(AAS),即可解决问题.
(1)如图1.过B作BE⊥AD于E,过B作BF⊥DC于F.
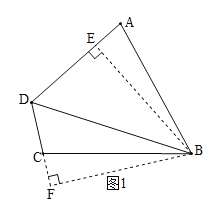
∵∠ABC+∠ADC=180°,∴∠A+∠DCB=180°.
∵∠DCB+∠FCB=180°,∴∠A=∠FCB.
∵BE⊥AD,BF⊥DC,∴∠AEB=∠CFB=90°.
在△AEB和△CFB中,∵∠A=∠FCB,∠AEB=∠CFB=90°,AB=CB,
∴△AEB≌△CFB,
∴BE=BF.
∵BE⊥AD,BF⊥DC,BE=BF,∴DB平分∠ADC;
(2)如图2中,在BD截取DE=AD,连接AE,
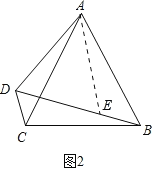
∵AB=CB,∠BAC=60°,∴△ABC是等边三角形,∴∠ABC=60°.
∵∠ABC+∠ADC=180°,∴∠ADC=120°.
由(1)得:DB平分∠ADC,∴∠ADB=∠CDB=60°.
∵DE=AD,∴△ADE是等边三角形,∴AD=DE=AE.
∵∠DAE=∠CAB=60°,∴∠DAC=∠BAE,
在△DAC与△EAB中,∵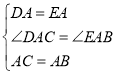 ,
,
∴△DAC≌△EAB(SAS),∴DC=BE.
∵BD=BE+DE,∴BD=AD+CD,
即BD﹣CD=AD.
(3)作EN∥DC交BD于N,在DF上截取DM=DC.
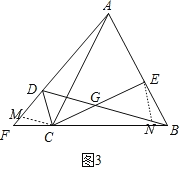
∵∠ADC=120°,∴∠CDM=60°.
∵DM=DC,∴△DMC是等边三角形,
∴CM=CD=DM,∠DMC=60°,∴∠FMC=120°.
∵CD∥EN,∴∠CDG=∠ENG=60°,
∴∠ENB=120°,∴∠CMF=∠ENB.
∵∠F+∠FBD=∠ADB=60°,∠FBD+∠EBN=60°,
∴∠F=∠EBN.
在△CFM和△EBN中,∵∠CMF=∠ENB,∠F=∠EBN,CF=BE,
∴△CFM≌△EBN(AAS),∴FM=BN,EN=CM=CD.
∵EN∥CD,∴∠CDG=∠GNE.
∵∠DGC=∠EGN,∴△DGC≌△NGE(AAS),
∴DG=GN=3,∴2BD=AF﹣FM+DN+BN=8+6=14,∴BD=7.


科目:初中数学 来源: 题型:
【题目】某商场代销甲、乙两种商品,其中甲种商品进价为120元/件,售价为130元/件,乙种商品进价为100元/件,售价为150元/件.
(1)若商场用36000元购进这两种商品若干,销售完后可获利润6000元,则该商场购进甲、乙两种商品各多少件?(列方程组解答)
(2)若商场购进这两种商品共100件,设购进甲种商品x件,两种商品销售后可获总利润为y元,请写出y与x的函数关系式(不要求写出自变量x的范围),并指出购进甲种商品件数x逐渐增加时,总利润y是增加还是减少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )

A. 7 B. 8 C. 7![]() D. 7
D. 7![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.
(1)求证:四边形BEDF是菱形;
(2)若正方形ABCD的边长为4,AE=![]() ,求菱形BEDF的面积.
,求菱形BEDF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(2,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动,当直线AB与⊙O相切时,A点的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 过原点和点
过原点和点![]() ,位于第一象限的
,位于第一象限的![]() 点在直线
点在直线![]() 上,
上,![]() 轴上有一点
轴上有一点![]() ,
,![]() ,
,![]() 轴于点
轴于点![]() .
.
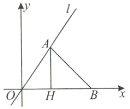
(1)求直线![]() 的解析式;
的解析式;
(2)求线段![]() 、
、![]() 的长度;
的长度;
(3)求![]() 点的坐标;
点的坐标;
(4)若![]() 点是线段
点是线段![]() 上一点,令
上一点,令![]() 长为
长为![]() ,
,![]() 的面积为
的面积为![]() .
.
①写出![]() 与
与![]() 的函数关系式,并指出自变量
的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
②当![]() 取何值时,
取何值时,![]() 为钝角三角形.
为钝角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com