
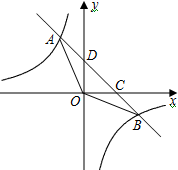
 如图,已知一次函数y=-x+1的图象与反比例函数$y=\frac{k}{x}$的图象交点A(-3,m)和B(n,-3),直线AB与x轴,y轴分别交于点C、点D.
如图,已知一次函数y=-x+1的图象与反比例函数$y=\frac{k}{x}$的图象交点A(-3,m)和B(n,-3),直线AB与x轴,y轴分别交于点C、点D.分析 (1)由点A的坐标,利用一次函数图象上点的坐标特征即可求出m值,从而得出点A的坐标,再根据点A的坐标利用反比例函数图象上点的坐标特征求出反比例函数解析式;
(2)将y=0代入直线AB解析式中求出点C的坐标,再结合三角形的面积公式以及S△AOB=S△AOC+S△BOC即可得出结论;
(3)由点B的坐标,利用一次函数图象上点的坐标特征即可求出n值,从而得出点B的坐标,再根据两函数图象的上下位置关系即可得出不等式的解集.
解答 解:(1)∵点A(-3,m)在一次函数y=-x+1的图象上,
∴m=-1×(-3)+1=4,
∴A(-3,4).
∵点A(-3,4)在反比例函数$y=\frac{k}{x}$的图象上,
∴4=$\frac{k}{-3}$,解得:k=-12,
∴反比例函数解析式为y=$\frac{-12}{x}$.
(2)令y=-x+1中y=0,则x=1,
∴C(1,0),
∴S△AOB=S△AOC+S△BOC=$\frac{1}{2}$OC•(yA-yB)=$\frac{1}{2}$×1×[4-(-3)]=$\frac{7}{2}$.
(3)∵点B(n,-3)在一次函数y=-x+1的图象上,
∴-3=-n+1,解得:n=4,
∴B(4,-3).
观察函数图象发现:当x<-3或0<x<4时,一次函数图象在反比例函数图象的上方,
∴不等式-$x+1-\frac{k}{x}>0$的解集为x<-3或0<x<4.
点评 本题考查了反比例函数图象上点的坐标特征、三角形的面积以及一次函数图象上点的坐标特征,解题的关键是:(1)求出点A的坐标;(2)根据S△AOB=S△AOC+S△BOC求出△AOB的面积;(3)根据两函数图象上下位置关系解不等式.本题属于中档题,难度不大,解决该题型题目时,根据一次函数图象上点的坐标特征求出点的坐标是关键.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在压力不变的情况下,某物体承受的压强P(Pa)是它的受力面积S(m2)的反比例函数,其图象如图所示.
在压力不变的情况下,某物体承受的压强P(Pa)是它的受力面积S(m2)的反比例函数,其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
| A. | (-4,-6) | B. | (-2,-2) | C. | (-1,-3) | D. | (0,-6) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 载重量 | 运往A地的费用 | 运往B地的费用 | |
| 大车 | 15吨/辆 | 630元/辆 | 750元/辆 |
| 小车 | 10吨/辆 | 420元/辆 | 550元/辆 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com