
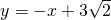 交y轴于点A,交x轴于点B,三角板OCD如图1置,其中∠D=30°,∠OCD=90°,OD=7,把三角板OCD绕点.顺时针旋转15°,得到△OC1D1(如图2),这时OC1交AB于点E,C1D1交AB于点F.
交y轴于点A,交x轴于点B,三角板OCD如图1置,其中∠D=30°,∠OCD=90°,OD=7,把三角板OCD绕点.顺时针旋转15°,得到△OC1D1(如图2),这时OC1交AB于点E,C1D1交AB于点F.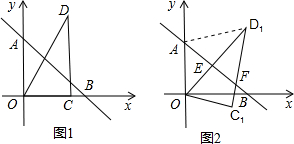
 ,
, ,
,
 OD2=3.5,
OD2=3.5, ,
, <
< ,
,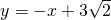 可知,∠OAB=45°,图(1)中,∠AOD=30°,由旋转15°可知,图(2)中∠AOE=45°,根据三角形的内角和定理可得∠AEO=90°,根据∠EFC1=∠D1+∠D1EF=∠D1+∠AEO,求解;
可知,∠OAB=45°,图(1)中,∠AOD=30°,由旋转15°可知,图(2)中∠AOE=45°,根据三角形的内角和定理可得∠AEO=90°,根据∠EFC1=∠D1+∠D1EF=∠D1+∠AEO,求解; ,可求OE=AE=3,故D1E=0D1-OE=4,在Rt△AED1中,利用勾股定理求AD1;
,可求OE=AE=3,故D1E=0D1-OE=4,在Rt△AED1中,利用勾股定理求AD1;

科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 点的坐标 | A | B | C | D | E |
| 点的横坐标x | -2 | 2 | |||
| 点的纵坐标y | -1 | 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:竞赛辅导:一次函数及绝对值函数的应用1(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com