
分析 根据题目中的式子变形可以求得x+$\frac{1}{x}$的值,然后将所求式子变形即可解答本题.
解答 解:∵x2-3x+1=0,
∴x-3+$\frac{1}{x}=0$,
∴x+$\frac{1}{x}$=3,
∴$\frac{{x}^{3}+\frac{1}{{x}^{3}}+7}{{x}^{4}+\frac{1}{{x}^{4}}+3}$
=$\frac{(x+\frac{1}{x})({x}^{2}-1+\frac{1}{{x}^{2}})+7}{({x}^{2}+\frac{1}{{x}^{2}})^{2}+1}$
=$\frac{(x+\frac{1}{x})[(x+\frac{1}{x})^{2}-3]+7}{[(x+\frac{1}{x})^{2}-2]^{2}+1}$
=$\frac{3×({3}^{2}-3)+7}{({3}^{2}-2)^{2}+1}$
=$\frac{25}{50}$
=$\frac{1}{2}$.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
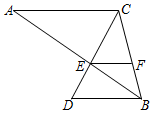 如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3.
如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com