

分析 (1)直接根据反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义求解;
(2)作OF⊥x轴垂足为F,作CE⊥PF与点E,作DH⊥CE与点H,交x轴与点G,则正方形OPCD分割成4个全等的直角三角形与一个正方形,设P(m,$\frac{2}{m}$),则
C(m+$\frac{2}{m}$,|$\frac{2}{m}-m$|),由S△OCM=S△OPF=1列出关于m的方程求其解,那么正方形的面积等于4个全等的直角三角形与一个正方形面积的和.
解答 解:(1)∵四边形OAPB是正方形
∴PA⊥y轴于点A,PB⊥x轴于B点,
∴矩形OAPB的面积=|2|=2.
故答案为:2;
(2)如下图2所示:作OF⊥x轴垂足为F,作CE⊥PF与点E,作DH⊥CE与点H,交x轴与点G,
易证:Rt△OFP≌Rt△PEC≌Rt△CHD≌Rt△DGO,且四边形EFGH为正方形
则:OF=PE=CH=DG,PF=CE=DH=OG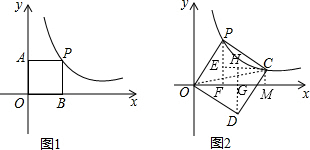
设P(m,$\frac{2}{m}$),C(m+$\frac{2}{m}$,|$\frac{2}{m}-m$|),
则:S△ODM=$\frac{1}{2}$(m+$\frac{2}{m}$)|$\frac{2}{m}-m$|=1
当0<m<$\sqrt{2}$时,S△OCM=$\frac{1}{2}$(m+$\frac{2}{m}$)($\frac{2}{m}-m$)=1,
即:$\frac{1}{2}$(m+$\frac{2}{m}$)($\frac{2}{m}-m$)=1
$\frac{4}{{m}^{2}}-{m}^{2}$=2…①
解①得:m2=$\sqrt{5}$-1
设正方形的边长为a,则其面积为a2,
则a=$\frac{2}{m}-m$,
a2=$\frac{4}{{m}^{2}}$+m2-4═$\frac{4}{{m}^{2}}$-m2+2m2-4=2m2-2=2$\sqrt{5}$-4
∴S正方形OPCD=4×1+a2=4+2$\sqrt{5}$-4=2$\sqrt{5}$,
当m$≥\sqrt{2}$时,$\frac{1}{2}$(m+$\frac{2}{m}$)(m-$\frac{2}{m}$)=1
m2-$\frac{4}{{m}^{2}}$=2…②
解②得:m2=$\sqrt{5}$+1
则a=m-$\frac{2}{m}$,
a2=$\frac{4}{{m}^{2}}$+m2-4═$\frac{4}{{m}^{2}}$-m2+2m2-4=2m2-6=2$\sqrt{5}$-4
∴S正方形OPCD=4×1+a2=4+2$\sqrt{5}$-4=2$\sqrt{5}$,
综上所述:正方形OPCD是面积为2$\sqrt{5}$
故答案为:2$\sqrt{5}$
点评 本题考查了反比例函数系数k的几何意义、正方形的性质,解题的关键是根据正方形的性质将正方形OPCD分割成4个全等的直角三角形与一个正方形.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=1-3x | C. | y=$\frac{1}{2x}$+2 | D. | y=$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
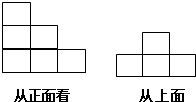 如图,是一个立体图形从两个不同方向看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数最多是( )
如图,是一个立体图形从两个不同方向看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数最多是( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
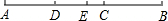 如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )
如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )| A. | 8cm | B. | 12cm | C. | 14cm | D. | 10cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
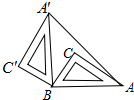 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )| A. | 10$\sqrt{2}$ | B. | 10 | C. | 20 | D. | 5$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com