
已知正方形ABCD中,边长为4,E为AB边上的一动点,(E与A,B点不重合),设AE=x,以E为顶点的内接正方形的面积为y,求y与x的函数关系式,当x为何值时内接正方形的面积最小.
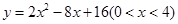 .当
.当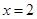 时,内接正方形的面积最小
时,内接正方形的面积最小
【解析】
试题分析:此题利用正方形的性质,求得△AEH≌△DHG≌△CFG≌△BEF,再利用勾股定理列出函数关系式就可以解决问题.
如图,
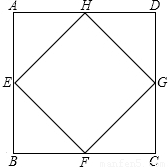
∵ABCD与EFGH均为正方形,
∴∠A=∠B=∠C=∠D,EF=FG=GH=HE,
∠DHG+∠AHE=∠DHG+∠DGH=∠BEF+∠AEH=∠BEF+∠BFE=∠BFE+∠GFC=90°,
∴∠AHE=∠DGH=∠GFC=∠BEF,
∴△AEH≌△DHG≌△CFG≌△BEF,
设AE=x,则BF=CG=DH=x,
BE=CF=DG=AH=4-x,
EF2=BE2+BF2=x2+(4-x)2=2x2-8x+16,
∴y=S正方形EFGH=EF2=2x2-8x+16=2(x-2)2+8≥8,
∴y与x的函数关系式为:y=EF2=2x2-8x+16,
当且仅当x=2,即E为AB中点时取最小值8.
考点:本题考查的是正方形的性质、三角形全等及二次函数的最值
点评:解答本题的关键是根据正方形的性质构建二次函数的模型,根据二次函数的最值解决问题.


科目:初中数学 来源: 题型:
 如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.
如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.查看答案和解析>>
科目:初中数学 来源: 题型:
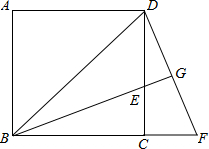 (2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.
如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com