
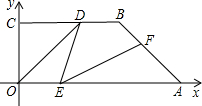
如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在x轴,y轴的正半轴上.OA∥BC,D是BC上一点,![]() ,AB=3, ∠OAB=45°,E,F分别是线段OA,AB上的两个动点,且始终保持∠DEF=45°,设OE=x,AF=y,则y与x的函数关系式为 ▲ ;如果△AEF是等腰三角形.△AEF沿EF对折得△A′EF与五边形OEFBC重叠部分的面积 ▲ .
,AB=3, ∠OAB=45°,E,F分别是线段OA,AB上的两个动点,且始终保持∠DEF=45°,设OE=x,AF=y,则y与x的函数关系式为 ▲ ;如果△AEF是等腰三角形.△AEF沿EF对折得△A′EF与五边形OEFBC重叠部分的面积 ▲ .
![]() 1、
1、 ![]() 、1、
、1、 ![]()
解析: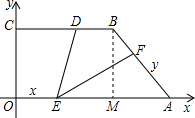
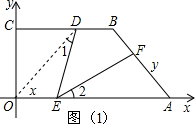 解:过B作BM⊥x轴于M;
解:过B作BM⊥x轴于M;
Rt△ABM中,AB=3,∠BAM=45°;则AM=BM=![]() ;
;
∴BC=OA-AM=4![]() -
-![]() =
=![]() ,CD=BC-BD=
,CD=BC-BD=![]() ;
;
连接OD;如图(1),由(1)知:D在∠COA的平分线上,则∠DOE=∠COD=45°;
又∵在梯形DOAB中,∠BAO=45°,
∴OD=AB=3
由三角形外角定理得:∠1=∠DEA-45°,又∠2=∠DEA-45°,
∴∠1=∠2,
∴△ODE∽△AEF,
∴![]() ,即:
,即:![]() ,
,
∴y与x的解析式为:![]() ,
,
当△AEF为等腰三角形时,存在EF=AF或EF=AE或AF=AE共3种情况;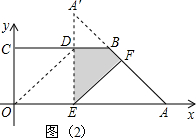
①当EF=AF时,如图(2),∠FAE=∠FEA=∠DEF=45°;
∴△AEF为等腰直角三角形,D在A′E上(A′E⊥OA),
B在A′F上(A′F⊥EF)
 ∴△A′EF与五边形OEFBC重叠的面积为四边形EFBD的面积;
∴△A′EF与五边形OEFBC重叠的面积为四边形EFBD的面积;
∵![]() ,
,
∴![]() ,
,
三角形AEF的面积=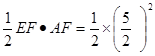 =
=![]()
∴四边形BDEF的面积=四边形AEDB的面积-三角形AEF的面积=![]() =
=![]()
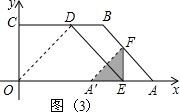
②当EF=AE时,如图(3),此时△A′EF与五边形OEFBC重叠部分面积为△A′EF面积.
∠DEF=∠EFA=45°,DE∥AB,又DB∥EA,
∴四边形DEAB是平行四边形
∴AE=DB=![]() ,
,
∴三角形![]() 的面积=三角形AEF的面积=
的面积=三角形AEF的面积=![]() =1
=1
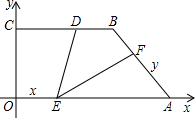
③当AF=AE时,如图(4),四边形AEA′F为菱形且△A′EF在五边形OEFBC内.
∴此时△A′EF与五边形OEFBC重叠部分面积为△A′EF面积.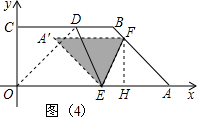
由(2)知△ODE∽△AEF,则OD=OE=3,
∴AE=AF=OA-OE=![]() ,
,
过F作FH⊥AE于H,则![]() ,
,
∴三角形![]() 的面积=
的面积=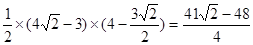 ,
,
综上所述,△A′EF与五边形OEFBC重叠部分的面积为![]() 或1或
或1或![]() .
.
故答案为:![]() ,
,![]() 或1或
或1或![]() .
.


科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=| k |
| x |
| BF |
| OA |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 是BC上一点,BD=
是BC上一点,BD=| 1 |
| 4 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com