
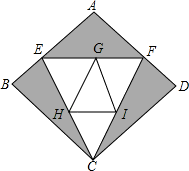
 种植成本降低了1成,使每平方米荷花和每平方米茉莉的种植总成本提高了8%.
种植成本降低了1成,使每平方米荷花和每平方米茉莉的种植总成本提高了8%.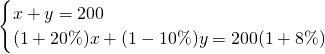

 x2+
x2+ ×8(8-x)×2]平方米.
×8(8-x)×2]平方米. x2-
x2- ×8(8-x)×2]×
×8(8-x)×2]× 平方米.
平方米. x2+
x2+ ×8(8-x)×2]×144+[82-
×8(8-x)×2]×144+[82- x2-
x2- ×8(8-x)×2]×
×8(8-x)×2]× ×72=7956
×72=7956 x2+
x2+ ×8(8-x)×2]平方米,再根据点G、H、I分别是EF、CE、CF的中点得到HI、GH、GI均为△CEF的中位线,然后表示出茉莉的种植面积,根据种植成本为7956元列出方程求得x的值即可求得AE的长.
×8(8-x)×2]平方米,再根据点G、H、I分别是EF、CE、CF的中点得到HI、GH、GI均为△CEF的中位线,然后表示出茉莉的种植面积,根据种植成本为7956元列出方程求得x的值即可求得AE的长.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
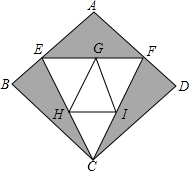 种植成本降低了1成,使每平方米荷花和每平方米茉莉的种植总成本提高了8%.
种植成本降低了1成,使每平方米荷花和每平方米茉莉的种植总成本提高了8%.查看答案和解析>>
科目:初中数学 来源:2013年贵州省黔西南州兴义市猪场坪乡中学中考数学模拟试卷(解析版) 题型:解答题
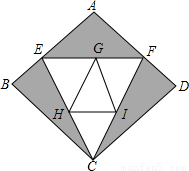
查看答案和解析>>
科目:初中数学 来源:2012年江苏省苏州市中考数学模拟试卷(五)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com