
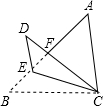
 如图,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4$\sqrt{2}$.
如图,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4$\sqrt{2}$.分析 ①如图作AM⊥BC于M.在Rt△ABM中,由∠AMB=90°,∠B=45°,推出BM=AM,AB=$\sqrt{2}$AM,设AM=BM=x,在Rt△AMC中,根据AC2=AM2+CM2,
可得方程52=x2+(4$\sqrt{2}$-x)2,求出x即可解决问题.
②如图作FN⊥BC于N.由△ACF∽△ABC,得到AC2=AF•AB,推出AF=$\frac{25}{7}$,BF=AB-AF=$\frac{24}{7}$,求出FN、CN,根据tan∠BCD=$\frac{FN}{CN}$计算即可.
解答 解:①如图作AM⊥BC于M.
在Rt△ABM中,∵∠AMB=90°,∠B=45°,
∴BM=AM,AB=$\sqrt{2}$AM,设AM=BM=x,
在Rt△AMC中,∵AC2=AM2+CM2,
∴52=x2+(4$\sqrt{2}$-x)2,
解得x=$\frac{7\sqrt{2}}{2}$或$\frac{\sqrt{2}}{2}$(舍弃),
∴AB=$\sqrt{2}$x=7,
故答案为7.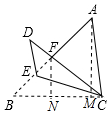
②如图作FN⊥BC于N.
∵DE∥AC,
∴∠ACF=∠D=∠B,∵∠CAF=∠CAB,
∴△ACF∽△ABC,
∴AC2=AF•AB,
∴AF=$\frac{25}{7}$,
∴BF=AB-AF=7-$\frac{25}{7}$=$\frac{24}{7}$,
∴BN=FN=$\frac{12\sqrt{2}}{7}$,
∴CN=BC-BN=4$\sqrt{2}$-$\frac{12\sqrt{2}}{7}$=$\frac{16\sqrt{2}}{7}$,
∴tan∠BCD=$\frac{FN}{CN}$=$\frac{\frac{12\sqrt{2}}{7}}{\frac{16\sqrt{2}}{7}}$=$\frac{3}{4}$,
故答案为$\frac{3}{4}$.
点评 本题考查翻折变换,解直角三角形、等腰直角三角形的性质、相似三角形的判定和性质等知识,解题的关键是学会用方程的思想思考问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
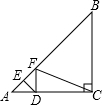 如图,在Rt△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,点E为AB上一动点,过点E作DE⊥AB交AC于D,将∠A沿 DE翻折,点A落在线段AB上的点F处,当△BCF为等腰三角形时,AE的长为$\frac{2-\sqrt{2}}{2}$或$\frac{1}{2}$.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,点E为AB上一动点,过点E作DE⊥AB交AC于D,将∠A沿 DE翻折,点A落在线段AB上的点F处,当△BCF为等腰三角形时,AE的长为$\frac{2-\sqrt{2}}{2}$或$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对保定市居民日平均用水量的调查 | |
| B. | 对乘坐飞机的旅客是否携带违禁物品的调查 | |
| C. | 对一个社区每天丢弃塑料袋数量的调查 | |
| D. | 对河北电视台“中华好诗词”栏目收视率的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
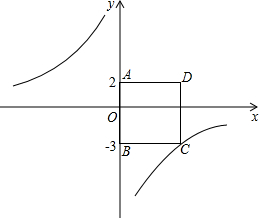 如图,在平面直角坐标系中,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=$\frac{k}{x}$的图象经过点C.
如图,在平面直角坐标系中,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=$\frac{k}{x}$的图象经过点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
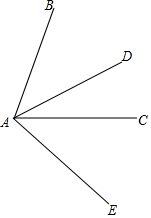 如图,∠BAC和∠DAE都是70°30′的角.
如图,∠BAC和∠DAE都是70°30′的角.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
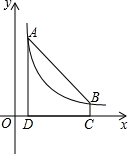 如图,点A(1,6)和点B在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(1,6)和点B在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com