
【题目】综合题。
(1)(﹣2)﹣1﹣|﹣ ![]() |+(3.14﹣π)0+4cos45°
|+(3.14﹣π)0+4cos45°
(2)已知x2﹣2x﹣7=0,求(x﹣2)2+(x+3)(x﹣3)的值.
【答案】
(1)
解:原式=﹣ ![]() ﹣2
﹣2 ![]() +1+2
+1+2 ![]() =
= ![]()
(2)
解:原式=x2﹣4x+4+x2﹣9=2x2﹣4x﹣5=2(x2﹣2x)﹣5,
∵x2﹣2x﹣7=0,即x2﹣2x=7,
∴原式=14﹣5=9
【解析】(1)原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及特殊角的三角函数值计算即可得到结果;(2)原式利用完全平方公式,平方差公式化简,去括号整理后,将已知等式变形后代入计算即可求出值.
【考点精析】解答此题的关键在于理解绝对值的相关知识,掌握正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离,以及对特殊角的三角函数值的理解,了解分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:
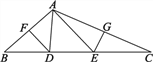
【题目】如图,△ABC中,∠BAC=110°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,BC=10cm.求:
(1)△ADE的周长;
(2)∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
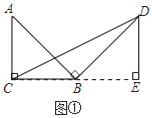
【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE, 易证△ABC≌△BDE,从而得到△BCD的面积为![]() .
.
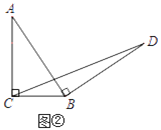
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
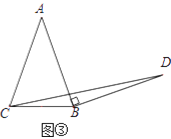
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,欢欢一家随旅游团到某风景区旅游,集体门票的收费标准是: ![]() 人以内(含
人以内(含![]() 人),每人
人),每人![]() 元;超过
元;超过![]() 人的,超过的部分每人
人的,超过的部分每人![]() 元.
元.
(![]() )写出应收门票费
)写出应收门票费![]() (元)与游览人数
(元)与游览人数![]() (人)(其中
(人)(其中![]() )之间的关系式.
)之间的关系式.
(![]() )利用(
)利用(![]() )中的关系式计算:若欢欢一家所在的旅游团共
)中的关系式计算:若欢欢一家所在的旅游团共![]() 人,那么该旅游团购门票共花了多少钱?
人,那么该旅游团购门票共花了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,已知点O是三个内角平分线的交点,OD∥AB,OE∥AC,则图中等腰三角形的个数是( )
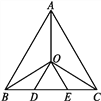
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.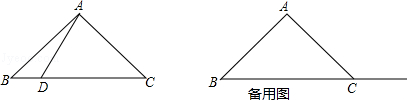
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB= ![]() ,则GE的长为
,则GE的长为 ![]() ,并简述求GE长的思路.
,并简述求GE长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.

(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计划拨款9万元从厂家购进50台电视机![]() 已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
![]() 若商场同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下商场的进货方案;
若商场同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下商场的进货方案;
![]() 若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元
若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元![]() 在同时购进两种不同型号电视机的方案中,为使销售时获利最多,你选择哪种进货方案;
在同时购进两种不同型号电视机的方案中,为使销售时获利最多,你选择哪种进货方案;
![]() 若商场准备用9万元同时购进三种不同的电视机50台,请你设计进货方案.
若商场准备用9万元同时购进三种不同的电视机50台,请你设计进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com