
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
(本题11分)如图所示,矩形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米(
厘米(![]() ).动点
).动点![]() 同时从
同时从![]() 点出发,分别沿
点出发,分别沿![]() ,
,![]() 运动,速度是
运动,速度是![]() 厘米/秒.过
厘米/秒.过![]() 作直线垂直于
作直线垂直于![]() ,分别交
,分别交![]() ,
,![]() 于
于![]() .当点
.当点![]() 到达终点
到达终点![]() 时,点
时,点![]() 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为![]() 秒.
秒.
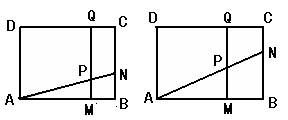
(1)若![]() 厘米,
厘米,![]() 秒,求PM的长度;
秒,求PM的长度;
(2)若![]() 厘米,求出某个时间
厘米,求出某个时间![]() ,使⊿PNB∽⊿PAD,并求出它们的相似比;
,使⊿PNB∽⊿PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:初中数学 来源:2012届湖北省随州市四校中考模拟联考数学卷(带解析) 题型:解答题
如图所示,直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,AB=3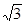 ,点M是BC的中点,点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P、Q的运动过程中,以PQ为边作等边△EPQ,使它与梯形ABCD在射线BC的同侧,点P、Q同时出发,点P返回到点M时停止运动,点Q也随之停止,设点P、Q运动的时间是t秒(t>0)。
,点M是BC的中点,点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P、Q的运动过程中,以PQ为边作等边△EPQ,使它与梯形ABCD在射线BC的同侧,点P、Q同时出发,点P返回到点M时停止运动,点Q也随之停止,设点P、Q运动的时间是t秒(t>0)。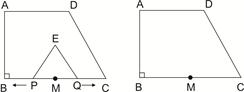
(1)设PQ的长为y,写出y与t之间的函数关系式(写出t的取值范围)。
(2)当BP=1时,求△EPQ与梯形ABCD重叠部分的面积。
(3)随着时间t的变化,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2011-2012学年四川新津县棕新中学八年级下学期期中考试数学卷(带解析) 题型:解答题
(本题11分)如图所示,矩形 中,
中,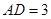 厘米,
厘米,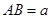 厘米(
厘米(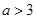 ).动点
).动点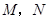 同时从
同时从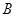 点出发,分别沿
点出发,分别沿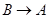 ,
, 运动,速度是
运动,速度是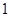 厘米/秒.过
厘米/秒.过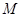 作直线垂直于
作直线垂直于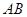 ,分别交
,分别交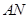 ,
, 于
于 .当点
.当点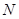 到达终点
到达终点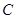 时,点
时,点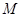 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为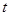 秒.
秒.
(1)若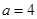 厘米,
厘米,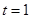 秒,求PM的长度;
秒,求PM的长度;
(2)若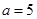 厘米,求出某个时间
厘米,求出某个时间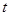 ,使⊿PNB∽⊿PAD,并求出它们的相似比;
,使⊿PNB∽⊿PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求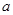 的取值范围;
的取值范围;
查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北省随州市四校中考模拟联考数学卷(解析版) 题型:解答题
如图所示,直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,AB=3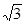 ,点M是BC的中点,点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P、Q的运动过程中,以PQ为边作等边△EPQ,使它与梯形ABCD在射线BC的同侧,点P、Q同时出发,点P返回到点M时停止运动,点Q也随之停止,设点P、Q运动的时间是t秒(t>0)。
,点M是BC的中点,点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P、Q的运动过程中,以PQ为边作等边△EPQ,使它与梯形ABCD在射线BC的同侧,点P、Q同时出发,点P返回到点M时停止运动,点Q也随之停止,设点P、Q运动的时间是t秒(t>0)。
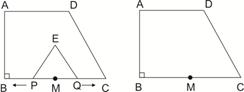
(1)设PQ的长为y,写出y与t之间的函数关系式(写出t的取值范围)。
(2)当BP=1时,求△EPQ与梯形ABCD重叠部分的面积。
(3)随着时间t的变化,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2013届四川新津县棕新中学八年级下学期期中考试数学卷(解析版) 题型:解答题
(本题11分)如图所示,矩形 中,
中, 厘米,
厘米,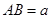 厘米(
厘米( ).动点
).动点 同时从
同时从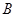 点出发,分别沿
点出发,分别沿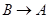 ,
,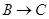 运动,速度是
运动,速度是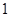 厘米/秒.过
厘米/秒.过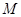 作直线垂直于
作直线垂直于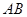 ,分别交
,分别交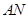 ,
,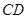 于
于 .当点
.当点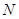 到达终点
到达终点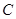 时,点
时,点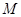 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为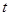 秒.
秒.
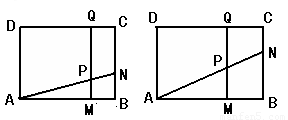
(1)若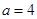 厘米,
厘米,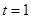 秒,求PM的长度;
秒,求PM的长度;
(2)若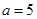 厘米,求出某个时间
厘米,求出某个时间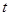 ,使⊿PNB∽⊿PAD,并求出它们的相似比;
,使⊿PNB∽⊿PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com