
 如图,在正方形PQRS中,M、N分别为QR、RS上的点,且∠MPN=30°.若△PMN为等腰三角形,且面积为1,则正方形PQRS的面积为________.
如图,在正方形PQRS中,M、N分别为QR、RS上的点,且∠MPN=30°.若△PMN为等腰三角形,且面积为1,则正方形PQRS的面积为________. 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
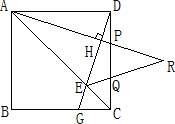 29、如图:在正方形ABCD中,点P、Q是CD边上的两点,且DP=CQ,过D作DG⊥AP于H,交AC、BC分别于E,G,AP、EQ的延长线相交于R.
29、如图:在正方形ABCD中,点P、Q是CD边上的两点,且DP=CQ,过D作DG⊥AP于H,交AC、BC分别于E,G,AP、EQ的延长线相交于R.查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏灌南实验中学九年级第一次阶段性检测数学试卷(带解析) 题型:解答题
如图:在正方形ABCD中,点P、Q是CD边上的两点,且DP=CQ,过D作DG⊥AP于H,交AC、BC分别于E,G,AP、EQ的延长线相交于R.
(1)求证:DP=CG;
(2)判断△PQR的形状,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏扬州宝应中南片七所学校初三12月月考数学试卷(解析版) 题型:解答题
如图:在正方形ABCD中,点P、Q是CD边上的两点,且DP=CQ,过D作DG⊥AP于H,交AC、BC分别于E,G,AP、EQ的延长线相交于R.

(1)求证:DP=CG;
(2)判断△PQR的形状,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏灌南实验中学九年级第一次阶段性检测数学试卷(解析版) 题型:解答题
如图:在正方形ABCD中,点P、Q是CD边上的两点,且DP=CQ,过D作DG⊥AP于H,交AC、BC分别于E,G,AP、EQ的延长线相交于R.
(1)求证:DP=CG;
(2)判断△PQR的形状,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 、EQ的延长线相交于R.
、EQ的延长线相交于R.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com