
 如图,一个动点A在平面直角坐标系中作折线运动,第一次从点(-1,-1)到A1(0,1),第二次运动到A2(3,-1),第三次运动到A3(8,1),第四次运动到A4(15,-1)…,按这样的运动规律,经过第13次运动后,动点A13的坐标是
如图,一个动点A在平面直角坐标系中作折线运动,第一次从点(-1,-1)到A1(0,1),第二次运动到A2(3,-1),第三次运动到A3(8,1),第四次运动到A4(15,-1)…,按这样的运动规律,经过第13次运动后,动点A13的坐标是 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
 (2012•开平区二模)如图,在梯形ABCD中,AD∥BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.连接BF、CF、AC.
(2012•开平区二模)如图,在梯形ABCD中,AD∥BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.连接BF、CF、AC.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•平南县二模)如图,在扇形EAB中,半径长AB=10,∠EAB=90°;以AB为直径作半圆O,点D是弧BE上的一个动点,BD与半圆O交于点C,DG⊥AB于点G,DG与AC交于点F,连结OF.
(2013•平南县二模)如图,在扇形EAB中,半径长AB=10,∠EAB=90°;以AB为直径作半圆O,点D是弧BE上的一个动点,BD与半圆O交于点C,DG⊥AB于点G,DG与AC交于点F,连结OF.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,将一块腰长为![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线![]() 上,
上,
1.点A的坐标为__________,点B的坐标为___________;抛物线的解析式为_________;
2.在抛物线上是否还存在点P(点B除外),使△ACP是以AC为直角边向直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由
3.若点D是(1)中所求抛物线在第三象限内的一个动点,连结BD、CD。当△BCD的面积最大时,求点D的坐标。
4.若点P是(1)中所求抛物线上一个动点,以线段AB、BP为邻边作平形四边形ABPQ。当点Q落在x轴上时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
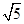 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线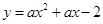 上,
上,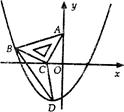
查看答案和解析>>
科目:初中数学 来源:2012届河南安阳九年级5月中考模拟考试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,将一块腰长为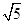 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线 上,
上,
【小题1】点A的坐标为__________,点B的坐标为___________;抛物线的解析式为_________;
【小题2】在抛物线上是否还存在点P(点B除外),使△ACP是以AC为直角边向直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由
【小题3】若点D是(1)中所求抛物线在第三象限内的一个动点,连结BD、CD。当△BCD的面积最大时,求点D的坐标。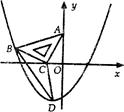
【小题4】若点P是(1)中所求抛物线上一个动点,以线段AB、BP为邻边作平形四边形ABPQ。当点Q落在x轴上时,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com