Question

3．设抛物线的解析式为y=ax²，过点B₁（1，0）作x轴的垂线，交抛物线于点A₁（1，2）；过点B₂（$\frac{1}{2}$，0）作x轴的垂线，交抛物线于点A₂；…；过点B_n（（$\frac{1}{2}$）^n-1，0）（n为正整数）作x轴的垂线，交抛物线于点A_n，连接A_nB_n+1，得Rt△A_nB_nB_n+1．
（1）求a的值；
（2）直接写出线段A_nB_n，B_nB_n+1的长（用含n的式子表示）；
（3）在系列Rt△A_nB_nB_n+1中，探究下列问题：
①当n为何值时，Rt△A_nB_nB_n+1是等腰直角三角形？
②设1≤k＜m≤n（k，m均为正整数），问：是否存在Rt△A_kB_kB_k+1与Rt△A_mB_mB_m+1相似？若存在，求出其相似比；若不存在，说明理由．

Answer 1

分析 （1）直接把点A₁的坐标代入y=ax²求出a的值；
（2）由题意可知：A₁B₁是点A₁的纵坐标：则A₁B₁=2×1²=2；A₂B₂是点A₂的纵坐标：则A₂B₂=2×（$\frac{1}{2}$）²=$\frac{1}{2}$；…则A_nB_n=2x²=2×[（$\frac{1}{2}$）^n-1]²=$（\frac{1}{2}）^{2n-3}$；
B₁B₂=1-$\frac{1}{2}$=$\frac{1}{2}$，B₂B₃=$\frac{1}{2}$-$（\frac{1}{2}）^{2}$=$\frac{1}{4}$=$（\frac{1}{2}）^{2}$，…，B_nB_n+1=$（\frac{1}{2}）^{n}$；
（3）因为Rt△A_kB_kB_k+1与Rt△A_mB_mB_m+1是直角三角形，所以分两种情况讨论：根据（2）的结论代入所得的对应边的比列式，计算求出k与m的关系，并与1≤k＜m≤n（k，m均为正整数）相结合，得出两种符合条件的值，分别代入两相似直角三角形计算相似比．

解答 解：（1）如图1所示，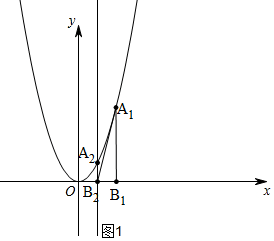

∵点A₁（1，2）在抛物线的解析式为y=ax²上，
∴a=2；
（2）如图2所示，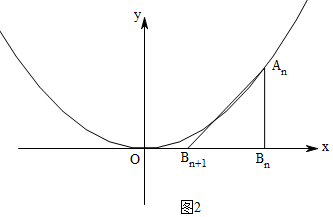

A_nB_n=2x²=2×[（$\frac{1}{2}$）^n-1]²=$（\frac{1}{2}）^{2n-3}$，B_nB_n+1=$（\frac{1}{2}）^{n}$；
（3）如图3所示，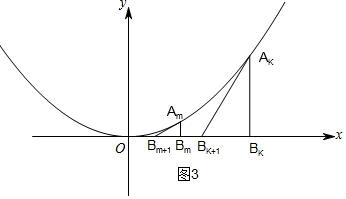

由Rt△A_nB_nB_n+1是等腰直角三角形得A_nB_n=B_nB_n+1，则：$（\frac{1}{2}）^{2n-3}$=$（\frac{1}{2}）^{n}$，
2n-3=n，n=3，
∴当n=3时，Rt△A_nB_nB_n+1是等腰直角三角形，
②依题意得，∠A_kB_kB_k+1=∠A_mB_mB_m+1=90°，
有两种情况：i）当Rt△A_kB_kB_k+1∽Rt△A_mB_mB_m+1时，
$\frac{{A}_{k}{B}_{k}}{{A}_{m}{B}_{m}}$=$\frac{{B}_{k}{B}_{k+1}}{{B}_{m}{B}_{m+1}}$，$\frac{（\frac{1}{2}）^{2k-3}}{（\frac{1}{2}）^{2m-3}}$=$\frac{（\frac{1}{2}）^{k}}{（\frac{1}{2}）^{m}}$，$（\frac{1}{2}）^{2k-2m}$=$（\frac{1}{2}）^{k-m}$，
所以，k=m（舍去），
ii）当Rt△A_kB_kB_k+1∽Rt△B_m+1B_mA_m时，
$\frac{{A}_{k}{B}_{k}}{{B}_{m+1}{B}_{m}}$=$\frac{{B}_{k}{B}_{k+1}}{{B}_{m}{A}_{m}}$，$\frac{（\frac{1}{2}）^{2k-3}}{（\frac{1}{2}）^{m}}$=$\frac{（\frac{1}{2}）^{k}}{（\frac{1}{2}）^{2m-3}}$，$（\frac{1}{2}）^{2k-3-m}$=$（\frac{1}{2}）^{k-2m+3}$，
∴k+m=6，
∵1≤k＜m≤n（k，m均为正整数），
∴取$\left\{\begin{array}{l}{k=1}\\{m=5}\end{array}\right.$或$\left\{\begin{array}{l}{k=2}\\{m=4}\end{array}\right.$；
当$\left\{\begin{array}{l}{k=1}\\{m=5}\end{array}\right.$时，Rt△A₁B₁B₂∽Rt△B₆B₅A₅，
相似比为：$\frac{{A}_{1}{B}_{1}}{{B}_{6}{B}_{5}}$=$\frac{2}{（\frac{1}{2}）^{5}}$=64，
当$\left\{\begin{array}{l}{k=2}\\{m=4}\end{array}\right.$时，Rt△A₂B₂B₃∽Rt△B₅B₄A₄，
相似比为：$\frac{{A}_{2}{B}_{2}}{{B}_{5}{B}_{4}}$=$\frac{\frac{1}{2}}{（\frac{1}{2}）^{4}}$=8，
所以：存在Rt△A_kB_kB_k+1与Rt△A_mB_mB_m+1相似，其相似比为64：1或8：1．

点评 本题考查了二次函数的综合问题，这是一个函数类的规律题，把坐标、二次函数和线段有机地结合在一起，以求线段的长为突破口，以相似三角形的对应边的比为等量关系，代入计算解决问题，综合性较强，因为本题小字标较多，容易出错．