
分析 利用二次根式的性质、二次根式的混合运算法则计算即可.
解答 解:(1)$\frac{\sqrt{72}-\sqrt{16}}{\sqrt{8}}$-($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)=$\frac{\sqrt{72}}{\sqrt{8}}$-$\frac{\sqrt{16}}{\sqrt{8}}$-(3-2)=3-$\sqrt{2}$-1=2$-\sqrt{2}$;
(2)$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$=3$\sqrt{2}$+$\sqrt{2}$-2$\sqrt{2}$=2$\sqrt{2}$.
点评 本题考查的是二次根式的混合运算,掌握二次根式的性质、二次根式的混合运算法则是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
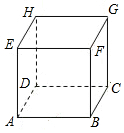 如图,一个上方无盖的正方体盒子紧贴地面,一只蚂蚁由盒外AE的中点处出发,沿着盒子面爬行到盒内的点C处,已知正方体的边长为4,问这只蚂蚁爬行的最短距离是10.
如图,一个上方无盖的正方体盒子紧贴地面,一只蚂蚁由盒外AE的中点处出发,沿着盒子面爬行到盒内的点C处,已知正方体的边长为4,问这只蚂蚁爬行的最短距离是10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
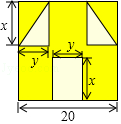 “囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
“囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3x}$与$\frac{a}{6{x}^{2}}$最简公分母是6x2 | |
| B. | $\frac{1}{3{a}^{2}{b}^{3}}$与$\frac{1}{3{a}^{2}{b}^{3}c}$最简公分母是3a2b3c | |
| C. | $\frac{1}{m+n}$与$\frac{1}{m-n}$的最简公分母是(m+n)(m-n) | |
| D. | $\frac{1}{a(x-y)}$与$\frac{1}{b(y-x)}$的最简公分母是ab(x-y)(y-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com