
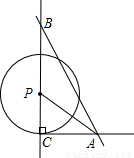
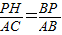
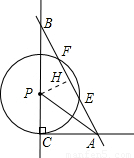
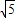 ,PH=
,PH=
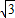 代入比例式得:PB=
代入比例式得:PB=
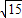 …(5分)
…(5分)
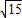 …(6分)
…(6分)
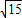 …(7分)
…(7分)
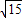 …(8分)
…(8分)
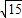 或8+
或8+
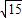 时,以⊙P与直线AB的两个交点和圆心P为顶点的三角形是正三角形.
时,以⊙P与直线AB的两个交点和圆心P为顶点的三角形是正三角形.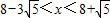 .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com