
 如图,正方形ABCD中,点E、F分别为AB、CD上的点,且AE=CF=$\frac{1}{3}$AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有3条.
如图,正方形ABCD中,点E、F分别为AB、CD上的点,且AE=CF=$\frac{1}{3}$AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有3条. 分析 能画3条:①与EF互相垂直且垂足为O,构建直角三角形,可以证明两直角三角形全等得EF=PQ;
②在AD上截取AP=$\frac{1}{3}$AD,连接PO延长得到PQ;
③同理在AB了截取BQ=$\frac{1}{3}$AB,连接QO并延长得到PQ.
解答 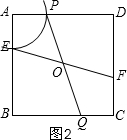
 解:这样的直线PQ(不同于EF)有3条,
解:这样的直线PQ(不同于EF)有3条,
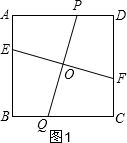
①如图1,过O作PQ⊥EF,交AD于P,BC于Q,
则PQ=EF;
②如图2,以点A为圆心,以AE为半径画弧,交AD于P,连接PO并延长交BC于Q,则PQ=EF;
③如图3,以B为圆心,以AE为半径画弧,交AB于Q,连接QO并延长交DC于点P,则PQ=EF.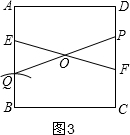
点评 本题考查了正方形的性质和全等三角形的性质与判定,本题虽然是做一条线段与EF相等,实际上是做好两件事:①画线段PQ,②能证明这两条线段相等,这比证明更为复杂,因此首先要构建直角三角形全等,找到与EF相等的边长的位置,本题的线段不止一条,容易丢解,要思考周全.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠B=50°,AE平分∠BAC,∠BAE=30°,则∠ACD=( )
如图,在△ABC中,∠B=50°,AE平分∠BAC,∠BAE=30°,则∠ACD=( )| A. | 100° | B. | 120° | C. | 135° | D. | 110° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8月10日 | B. | 10月12日 | C. | 1月20日 | D. | D、12月8日 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,两个标有数字的轮子可以分别绕中心旋转,旋转停止时,每个轮子上的箭头各指向轮子上的一个数字,若左图上方箭头指着的数字为a,右图中指着的数字为b.数对(a,b)所有可能的个数为n,其中a+b恰为偶数的不同数对个数为m,则$\frac{m}{n}$等于( )
如图,两个标有数字的轮子可以分别绕中心旋转,旋转停止时,每个轮子上的箭头各指向轮子上的一个数字,若左图上方箭头指着的数字为a,右图中指着的数字为b.数对(a,b)所有可能的个数为n,其中a+b恰为偶数的不同数对个数为m,则$\frac{m}{n}$等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{12}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com