
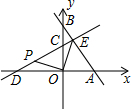
 如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,直线y=kx+3分别与x轴、y轴交于D、C两点,且CD=AB.
如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,直线y=kx+3分别与x轴、y轴交于D、C两点,且CD=AB.分析 (1)可先由直线解析式求得A、B坐标,则可求得AB的长,用k可表示出D点坐标,由CD=AB可得到关于k的方程,可求得k的值;
(2)①可先证△AOB≌△COD,进一步可证明△OBE≌△ODP,则可得△OPE为等腰直角三角形,过O作OF⊥CD于点F,则可知PE=2OF,利用等积法可求得OF的长,则可求得PE的长;②由条件可求得PQ∥AB,且DE⊥AB,利用平行线分线段可求得PE的长,即为P到AB的距离.
解答 解:
(1)在y=-$\frac{4}{3}$x+4中,令y=0可求得x=3,令x=0可求得y=4,
∴OA=3,OB=4,
∴AB=5,
在y=kx+3中,令y=0可得x=-$\frac{3}{k}$,令x=0可得y=3,
∴OC=3,OD=$\frac{3}{k}$,
∵CD2=OC2+OD2,即9+$\frac{9}{{k}^{2}}$=25,解得k=-$\frac{3}{4}$(舍去)或k=$\frac{3}{4}$,
即k的值为$\frac{3}{4}$;
(2)①由(1)可知OD=4,
在△AOB和△COD中
$\left\{\begin{array}{l}{OA=OC}\\{∠AOB=∠COD}\\{OB=OD}\end{array}\right.$
∴△AOB≌△COD(SAS),
∴∠ABO=∠CDO,
在△OBE和△ODP中
$\left\{\begin{array}{l}{OB=OD}\\{∠OBE=∠ODP}\\{BE=DP}\end{array}\right.$
∴△OBE≌△ODP(SAS),
∴OP=OE,∠BOE=∠POD,
∴∠POE=∠BOE+∠POC=∠POD+∠POC=∠DOC=90°,
∴△POE为等腰直角三角形,
过O作OF⊥DE于点F,如图1,则PE=2OF,
在Rt△OCD中,S△OCD=$\frac{1}{2}$OC•OD=$\frac{1}{2}$CD•OF,
∴3×4=5OF,解得OF=$\frac{12}{5}$,
∴PE=2OF=$\frac{24}{5}$;
②当△DPQ≌△DOC时,如图2,则∠DPQ=∠COD=90°,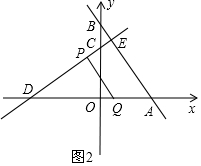
又∠EDA=∠ABO,
∴∠EDA+∠BAO=∠ABO+∠BAO=90°,
∴∠DEA=90°,
∴PQ∥AE,
∴$\frac{DP}{PE}$=$\frac{DQ}{AQ}$,
由题意可知OD=4,OA=3,OC=3,
∴DP=OD=4,DQ=DC=5,
∴AQ=DA-DQ=3+4-5=2,
∴$\frac{4}{PE}$=$\frac{5}{2}$,解得PE=$\frac{8}{5}$,
即点P到AB的距离为$\frac{8}{5}$.
点评 本题为一次函数的综合应用,涉及函数图象与坐标轴的交点、全等三角形的判定和性质、等腰直角三角形的判定和性质、勾股定理、平行线分线段成比例及等积法等知识.在(1)中求得OA、OB、OC、OD的长是解题的关键,在(2)①中证得△POE为等腰直角三角形是解题的关键,注意等积法的应用,在(2)②中确定出P到AB的距离是解题的关键.本题考查知识点较多,综合性较强,难度适中.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:解答题
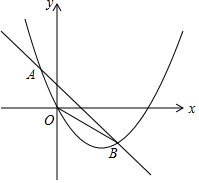 如图,在平面直角坐标系中,抛物线y=x2-bx与直线交于点A(-$\frac{1}{2}$,m),B(1,n),其中m>0,n<0,
如图,在平面直角坐标系中,抛物线y=x2-bx与直线交于点A(-$\frac{1}{2}$,m),B(1,n),其中m>0,n<0,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学为响应2017年万州区委、区府喜迎世界读书日“全面阅读,书香万州”建设的号召,在全校形成良好的人文阅读,该中学随机调查了八年级部分学生平均每天的阅读时间,统计结果如图所示:
某中学为响应2017年万州区委、区府喜迎世界读书日“全面阅读,书香万州”建设的号召,在全校形成良好的人文阅读,该中学随机调查了八年级部分学生平均每天的阅读时间,统计结果如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
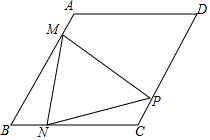 在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.
在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 22 | B. | 21 | C. | 20 | D. | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com