
 运动时心跳速率通常和人的年龄有关,用a表示一个人的年龄,用b表示正常情况下这个人在运动时所能承受的每份周心跳的最高次数,则b=0.8(220-a)
运动时心跳速率通常和人的年龄有关,用a表示一个人的年龄,用b表示正常情况下这个人在运动时所能承受的每份周心跳的最高次数,则b=0.8(220-a)分析 (1)把a=14代入公式计算求出b的值即可;
(2)设一个人的年龄为x岁,增加10岁为(x+10)岁,分别求出运动时承受的每分钟心跳的最高次数,求出差值即可得到结果.
解答 解:(1)当a=14时,该少年运动时所能承受的每分钟心跳的最高次数是b=0.8×(220-14)=164.8≈164;
(2)如果一个人的年龄为x岁,他运动时承受的每分钟心跳的最高次数是0.8(220-x);
当这个人的年龄增加10岁时,他运动时承受的每分钟心跳的最高次数是0.8×[220-(x+10)],
由于0.8×[220-(x+10)]-0.8(220-x)=-8,
所以,当一个人的年龄增加10岁时,他运动中承受的每分钟心跳的最高次数减少,减少的次数是8次.
点评 此题考查了代数式求值,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
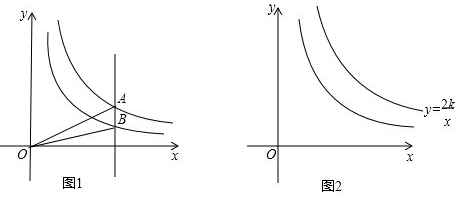
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
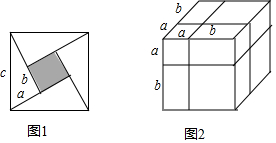 【知识生成】我们已经知道,通过不同的方法表示同一图形的面积,可以探求相应的等式.
【知识生成】我们已经知道,通过不同的方法表示同一图形的面积,可以探求相应的等式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,OA=3,OC=4,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
如图,在直角坐标系中,OA=3,OC=4,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com