
二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣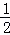 x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.

科目:初中数学 来源: 题型:
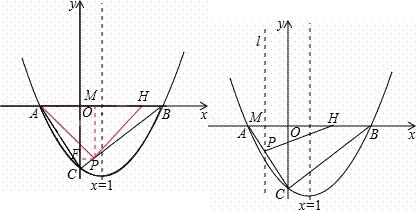
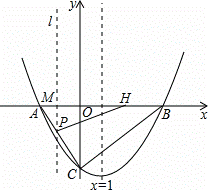
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.
(1)求抛物线的解析式;
(2)若两动点M,H分别从点A,B以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到达原点时,点H立刻掉头并以每秒 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,经过点M的直线l⊥x轴,交AC或BC于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,经过点M的直线l⊥x轴,交AC或BC于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
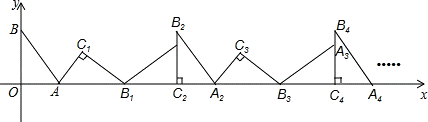
如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(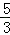 ,0),B(0,4),则点B2014的横坐标为 .
,0),B(0,4),则点B2014的横坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com